Giocando con il caos
La mia implementazione del circuito di Chua
Un primo tentativo con una induttanza reale
Una versione più configurabile con un GIC
Il mio circuito definitivo in azione
Conclusioni
Bibliografia
Traduzione in italiano gentilmente fatta da "elfo".
Video 1: L'uscita del mio circuito definitivo in commutato in "veloce", tracciato sullo schermo di un oscilloscopio analogico in modalità XY. Ulteriori video sotto!
Introduzione
Nell'autunno del 1987, andai con i miei genitori a Torino per visitare un'esposizione dedicata a Jean Tinguely. Quel giorno, seduto dietro in auto, probabilmente ero un annoiato bambino di 8 anni, inconsapevole di cosa fosse una "esposizione di arte contemporanea". Quando i miei genitori acquistarono i biglietti ed entrammo nella grande sala dell'esposizione fui immediatamente attratto dal mondo dadaista di Tinguely, fatto di macchine dall'aspetto bizzarro. Amavo quei meccanismi complicati, movimenti senza un apparente scopo pratico. Tra le altre cose, ho un vivo ricordo di una macchina per disegnare dove i bambini potevano mettere un foglio di carta e lasciare che la macchina disegnasse per loro. Vorrei aver conservato il mio! Fui cosi impressionato che detti il nome di Tinguely al mio pesce rosso che, di lì a poco, sarebbe diventato il mio animale domestico. Il ricordo di questa esperienza mi è ritornato in mente quasi trenta anni dopo, in modo piuttosto inatteso, in una calma sera autunnale spesa a giocare con i circuiti analogici caotici.
Il circuito di Chua è stato il primo circuito elettronico (inventato nel 1983 [1]) in cui fosse visibile il comportamento caotico. È un semplice oscillatore che genera segnali non-periodici. Si accede facilmente a due tensioni che sono di solito tracciate su un oscilloscopio in modalità XY e che producono un caratteristico attrattore conosciuto come "double scroll".
In questo articolo descrivo il circuito di Chua che ho costruito. A proposito, ho trovato molti esempi per gli oscilloscopi, ma oggi sembra che l'uso di un plotter analogico XY sia molto meno comune. Osservarli è in qualche modo ipnotico e mi rimanda a quelle macchine per disegnare che mi avevano cosi divertito quando ero trenta anni più giovane.
Questo articolo è organizzato come segue. Inizialmente descriverò la versione standard del circuito che impiega una induttanza. Poi mostrerò una versione dove l'induttanza è sostituita con un circuito Convertitore di Impedenza Generalizzato (GIC). Infine farò vedere alcuni dei video che ho registrato con il circuito in azione.
Un primo tentativo, con una induttanza reale
Il primo circuito che ho sperimentato è piuttosto classico ed è mostrato in figura 1 (a proposito, se può interessare, è disegnato con FidoCadJ). Il componente più critico del circuito è l'induttanza. Comunque tra i miei componenti di scorta ne ho un certo numero e ne ho scelta una con un valore ragionevolmente vicino a quelli impiegati in circuiti sicuramente funzionanti (come in [2], ma Internet è letteralmente pieno di circuiti di Chua, quindi GIYF, Google Is Your Friend - Google è tuo amico).
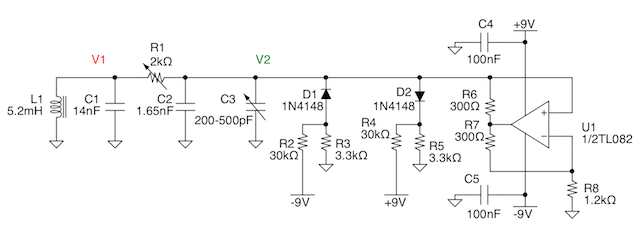
Fig.1: Il primo circuito di Chua con una induttanza reale (click per ingrandire). Qui il codice sorgente di FidoCadJ.
Il circuito di Chua è così famoso che ha una propria voce su Wikipedia [3], che riporta le equazioni che risultano dall'analisi del circuito:
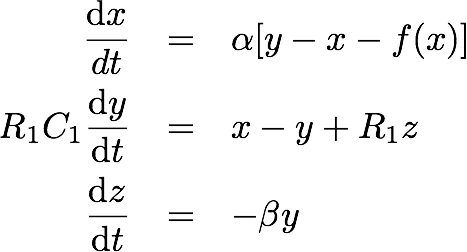
dove x(t) e y(t) sono rispettivamente le tensioni sulle capacità C2 e C1 e z(t) è la corrente nell'induttanza L1. I parametri α e β dipendono dalle scelte fatte nel resto del circuito e la non linearità è espressa nella caratteristica non lineare di f(x).
Infatti l'induttanza dovrebbe avere un valore relativamente grosso senza avere una eccessiva resistenza serie parassita. R1 controlla la regolazione del circuito e, per fornire un ulteriore grado di libertà, ho messo C3, un vecchio condensatore variabile in parallelo con la capacità C2. Questo non è obbligatorio, ma permette in qualche modo di cambiare la figura disegnata sullo schermo. D1, D2 e R2-R5 forniscono il comportamento non lineare del circuito come è richiesto per avere un comportamento caotico. I primi risultati non sono stati oltremodo impressionanti, ma hanno mostrato che il comportamento caotico era indubbiamente possibile, come mostrato in figura 2.
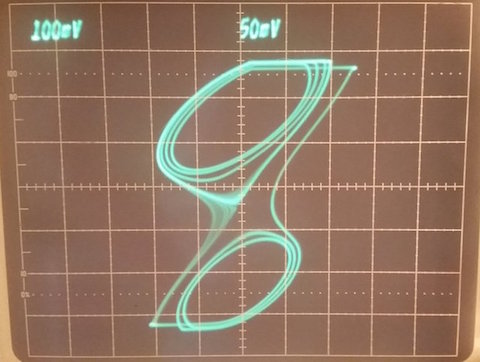
Fig.2: Il primo risultato che ho ottenuto giocando con il circuito mostrato in fig. 1 e un oscilloscopio in modalità XY. Non molto spettacolare, ma oh, è caotico!
In quel momento, avrei potuto tentare di migliorare il circuito che avevo, ma poiché il mio obiettivo era di provare ad usare un plotter analogico XY che avevo, ho deciso di cambiare strategia. Infatti, incrementare la costante di tempo del circuito avrebbe significato incrementare il valore dell'induttanza a valori totalmente impraticabili. Perciò ho adottato un Convertitore di Impedenza Generalizzato (GIC) per simulare l'induttanza, invece di usarne una reale. Questa non è una idea nuova, naturalmente, ed è risultata una buona scelta come vedremo nei seguenti paragrafi.
Una versione più configurabile con un GIC
Il GIC di Antoniou è un modo classico con cui può essere simulata una induttanza per mezzo di un semplice circuito che impiega due amplificatori operazionali [4]. Poiché il valore finale dell'induttanza dipenderà dal valore di altri componenti, è facile variare tale valore per mezzo di un semplice potenziometro. Questo aggiunge un grado di libertà molto utile che può essere sfruttato nel circuito. La mia implementazione è mostrata in figura 3.
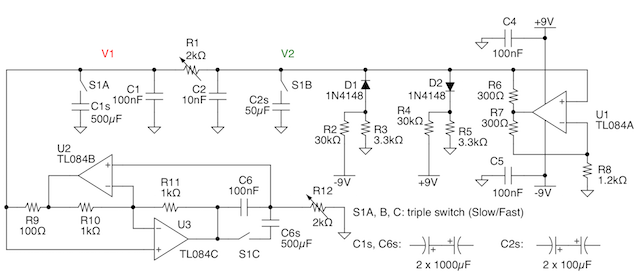
Fig.3: 3 Il secondo circuito di Chua, con l'induttanza simulata con un GIC (click per ingrandire). Qui il codice sorgente di FidoCadJ.
Il valore dell'induttanza è dato dalla seguente equazione:
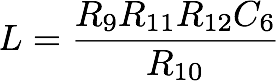 Il triplo interruttore S1 è utilizzato per incrementare di più di tre ordini di grandezza le capacità che sono impiegate nel circuito. In questo modo le costanti di tempo sono incrementate della stessa quantità e il comportamento del circuito è proporzionalmente più lento. Utilizzando la precedente equazione, imponendo 1 kΩ per R12 otteniamo una induttanza simulata di 10 mH quando l'interruttore è aperto, valore che aumenta fino a 50 H quando S1 è chiuso! Questo permette di ottenere quello di cui ho bisogno, cioè di disegnare il risultato con un plotter XY.
Il triplo interruttore S1 è utilizzato per incrementare di più di tre ordini di grandezza le capacità che sono impiegate nel circuito. In questo modo le costanti di tempo sono incrementate della stessa quantità e il comportamento del circuito è proporzionalmente più lento. Utilizzando la precedente equazione, imponendo 1 kΩ per R12 otteniamo una induttanza simulata di 10 mH quando l'interruttore è aperto, valore che aumenta fino a 50 H quando S1 è chiuso! Questo permette di ottenere quello di cui ho bisogno, cioè di disegnare il risultato con un plotter XY.
Il mio circuito definitivo in azione
Dopo una prova coronata da successo su una basetta sperimentale, ho messo il circuto di fig.3 in un piccolo contenitore di plastica che avevo comprato alcuni anni fa. Ho messo i potenziometri R1 e R2 sul pannello frontale insieme all'interruttore S1 e i due connettori BNC di uscita per i segnali X e Y (V1 e V2 nello schema di fig 3). La figura 4 mostra il risultato.

Fig.4: Il circuito nel contenitore, pronto per l'azione!
Le incisioni sul pannello frontale sono una stampa laser su un normale foglio di carta, tagliato a misura, plastificato e poi incollato sul contenitore di plastica come mostrato in figura 5. Tale semplice tecnica porta a risultati soddisfacenti per semplici progetti casalinghi come questo.

Fig.5: Ho stampato il pannello frontale con la mia stampante laser, l'ho plastificato e incollato sulla faccia superiore del contenitore. Tecnica semplice e ragionevolmente efficace per piccoli progetti come questo.
Quello che non è dettagliato è il circuito di alimentazione duale +/- 9 V che funziona a partire da un singolo ingresso a 9 VAC. Il trasformatore di rete è esterno al contenitore. Nel mio caso, avevo diversi LM723 sparsi nel cassetto e ne ho usati due per stabilizzare le tensioni di alimentazione positive e negative, con circuiti presi direttamente dal datasheet dell'LM723; niente di molto sofisticato ma funziona piuttosto bene. Figura 6 mostra il circuito finito, montato su una basetta millefori. Probabilmente, sarebbe più conveniente adottare un'alimentazione singola a 18 V ed ottenere un riferimento a 9 V con un partitore resistivo seguito da un inseguitore fatto con l'operazionale inutilizzato che rimane nel TL084.

Fig.6: Il circuito su un basetta millefori. È il circuito mostrato in Fig. 3 con una alimentazione duale ottenuta con due LM723.
C1s, C2s e C6s sono condensatori elettrolitici non polarizzati e sono ottenuti mettendo in anti-serie due condensatori identici di valore doppio di quello che si vuole ottenere. Questi condensatori sono montati direttamente dietro il pannello frontale, come mostrato in figura 7. Tutti i collegamenti sono realizzati con un semplice connettore così che il circuito rimane accessibile.

Fig.7: Il retro del pannello frontale. I grossi condensatori neri sono per la modalità "lenta" e R1 è un potenziometro a 10 giri.
Il video 2 mostra quello che volevo ottenere: l'attrattore a doppio scorrimento di Chua disegnato per mezzo di un vecchio plotter analogico XY. Penso che Tinguely lo avrebbe apprezzato, anche se manca della potenza dadaistica delle sue oltremodo complicate macchine alla Rube-Goldberg. Ma, dopo tutto, io non sono un artista! Adesso ho una piccola collezione di attrattori di Chua plastificati!
Video.2: Ecco un video del mio circuito connesso ad un plotter XY di un tempo. Personalmente ho trovato che osservare il plotter mentre disegna un attrattore è piuttosto ipnotizzante...
Ho sempre ammirato la memoria analogica a fosfori degli oscilloscopi Tektronix di un tempo e ho ovviamente provato a tracciare un attrattore con uno di questi, come mostrato nel video 3. I risultati son piuttosto piacevoli, almeno per i miei gusti.
Video.3: L'uscita del circuito (una versione leggermente più veloce) registrata su un oscilloscipio Tektronix a memoria analogica a fosfori.
Conclusioni
In questo articolo ho descritto come ho giocato con la mia implementazione del circuito di Chua. All'inizio sono partito con un semplice circuito con una induttanza reale, poi ho utlizzato un GIC per emularla. In questa seconda versione ho potuto beneficiare di un maggior campo di regolazione del circuito e ho potuto rallentarlo considerevolmente, in modo da poter impiegare un plotter XY per disegnare gli attrattori.
Mi sono divertito molto giocando con questo circuito. L'ho mostrato a due bambini figli di una coppia di amici e gli è piaciuto molto: il plotter produceva due strani attrattori per loro ed eravamo tutti felici. Guardare i video del plotter è certamente ipnotizzante e io mi sono sicuramente goduto il tempo speso.
Bibliografia
[1] - L.O. Chua "The genesis of Chua's Circuit" AEU, vol.46, n°4, 1992 (available online here)[2] - http://www.chuacircuits.com
[3] - Wikipedia's entry about Chua's circuit
[4] - S. Franco, "Design with Operational Amplifiers and Integrated Circuits" fourth edition, McGraw-Hill Education, New York, 2015
This article is also treated in a discussion (in italian language) on the ElectroYou forum. I would like to thank those who have found errors in this page!
Log:
November 11, 2016 - First version of the page, in English
November 12, 2016 - Correction of several typos (antiparallel -> antiseries, 100mH->10mH, error in fig. 3) and added more information on the inductance calculation.
November 14, 2016 - Typo correction, Italian translation from elfo. Corrected another stupid error in the schematic of fig. 3 (thanks IsidoroKZ!!!). Added a hint about power supply by GuidoB.
License

This work is licensed under a CC BY, NC 4.0 licence.
