Mathématiques
Même si je ne suis pas un mathématicien au sens stricte du terme, j'ai toujours été très attiré par les mathématiques. J'ai donc décidé d'y dédier une section de mon site.
|
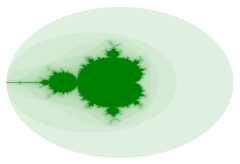
Introduction aux principes des fractales de Mandelbrot et de Julia (1998-2002), ITCet article, écrit désormais il y a beaucoup de temps, décrit brièvement certaines propriétés et propose une méthode pour dessiner les ensembles de Mandelbrot et de Julia sur l'écran d'un ordinateur. |
|
|
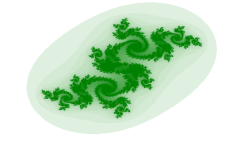
Fractales de Mandelbrot et de Julia en Java (2004), FR, ITUn exemple de ceux que l'on peut obtenir à l'aide des techniques décrites dans l'intervention précédente. Voici deux petites appliquettes Java (dont je publie le code source), utiles pour dessiner directement à l'intérieur du navigateur les ensembles de Mandelbrot et de Julia. |
|
|
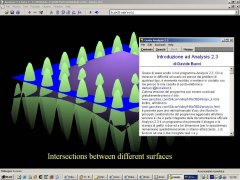
Analsysis 2.3beta2 (1998-2002), FR, ITAnalysis est un logiciel pour Windows que j'ai écrit. Il peut être utile pour tracer les graphiques de fonctions. J'ai travaillé à ce logiciel pendant plusieurs années, jusqu'en 2002, et il est intéressant encore aujourd'hui, pour son agilité et sa simplicité d'utilisation. |
|
|
Une introduction à Maxima (2007), FR, ITMaxima est une version OpenSource (sous la licence GPL) de Macsyma, le premier programme de manipulation algébrique développé au MIT entre la fin des années soixante et le début des années quatre-vingt du siècle dernier. J'ai recueilli et commenté certains exemples d'utilisation, qui permettent de se former une idée des possibilités énormes de ce logiciel. |
|
|
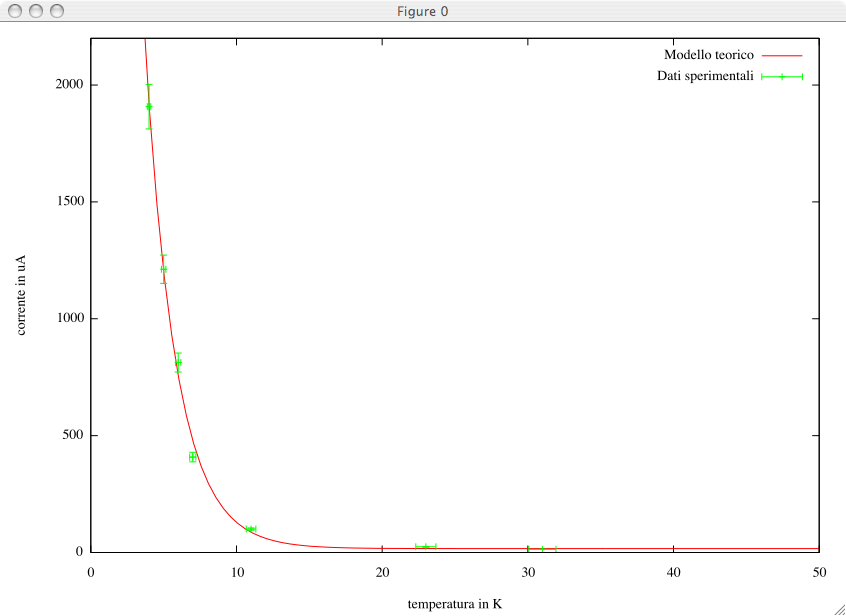
Une introduction a Gnuplot (2007-2008), FR, ITGnuplot est un logiciel très utile pour tracer des graphiques scientifiques assez hétérogènes. S'il est utilisé correctement, il peut fournir des résultats de type professionnel, souvent bien supérieures à ceux obtenus par exemple avec Excel. Dans cet article, nous allons voir quelques exemples d'utilisation plus ou moins avancés. |
|

|
The mathematical symmetry of the differential pair (2011)Article tiré de mon blog sur le site italien ElectroYou. Cette étude est dédiée à la paire différentielle. En particulier, on montre que l'on peut représenter l'effet du circuit sur les signaux en entrée à l'aide d'une multiplication d'une matrice fois un vecteur. On y demontre ensuite que les notions de mode commun et mode différentiel sont étroitement liées aux valeurs propres et vecteurs propres de dite matrice. Cet article est disponible seulement en Anglais et a été publié quelques jours avant Noël 2011. |
