Introduzione ai frattali di Mandelbrot e di Julia

Nota del 29 dicembre 2022: State per leggere uno dei primissimi articoli che ho scritto e messo online nella prima versione del sito caricata su Geocities nell'ormai lontano agosto del 1998 (ho trovato su Internet Wayback Machine una versione del 2001). Sembra che qualcuno cerchi ancora informazioni sull'argomento, spero che possa essere utile. All'epoca c'erano anche degli esempi in Visual Basic per DOS!

Introduzione
Cos'è un "frattale"?
Una vista sul piano complesso
Gli insiemi di Julia
L'insieme di Mandelbrot
Conclusioni

Introduzione

Spesso, soprattutto in questi ultimi anni, capita di imbattersi nelle elaborate e sicuramente affascinanti immagini chiamate, con un nome un po' curioso, frattali. Osservando queste immagini, viene da chiedersi quale misterioso segreto matematico esse racchiudano e quali siano le loro caratteristiche. Questo documento è stato elaborato allo scopo di spiegare, anche se non in maniera eccessivamente approfondita, due delle principali famiglie di frattali che possono venire rappresentati, ovvero gli insiemi di Julia e l'insieme di Mandelbrot. Per la lettura di questo documento, è consigliabile avere una conoscenza anche approssimativa della matematica complessa (che, in fondo, per quel che serve a noi, non è affatto tale!).

Cos'è un "frattale"?

Per essere riconosciuto come tale, un frattale deve possedere alcune caratteristiche fondamentali: La geometria frattale è di recente concezione (i primi studi sono quelli di G. Julia all’inizio del ventesimo secolo) e, solo con l’avvento dei calcolatori, che hanno offerto la necessaria potenza di calcolo, si è potuti giungere alle  affascinanti immagini generate dalle formule. Negli anni ottanta, si è spesso tentato di vedere in tutte le cose un frattale (uno dei libri più importanti sui frattali si intitola appunto The Fractal Geometry of Nature, la geometria frattale della natura, di Benoit Mandelbrot pubblicato nel 1982). Si è sviluppata quindi una branca della geometria frattale che studia i cosiddetti frattali biomorfi, cioè simili ad oggetti presenti in natura. I risultati a volte sono stati stupefacenti. Uno dei frattali biomorfi infatti più riusciti è la foglia di felce i cui dettagli, detti autosimili, riproducono sempre la stessa figura. Nella rivista di divulgazione “Le Scienze”, sono apparsi negli anni diversi articoli proprio sui frattali biomorfi, che spiegano meglio alcuni aspetti più matematici dell’analisi delle forme. Uno dei principali limiti dell’applicazione dei frattali allo studio della natura è che, seppure essi descrivano in modo soddisfacente la struttura globale, non possono essere precisi fino al dettaglio; “un ago di pino è strutturalmente diverso dai rami e dal tronco dello stesso albero” scrive Giorgio Meini  in un articolo apparso su Computer Programming n°42 (Dicembre 1995). Insomma, lo studio delle affinità fra la natura ed i frattali può rivelare curiose analogie, ma spesso soltanto casuali.

I principi dei frattali

Iniziamo ora ad addentrarci un poco più approfonditamente nel mondo della matematica dei frattali. Una caratteristica comune alle due famiglie di frattali che analizzeremo (esistono molti tipi diversi di frattali) è che sono degli insiemi di punti che soddisfano determinati requisiti, come vedremo in seguito. Poichè abbiamo parlato di punti, sorge naturale il quesito di dove questi punti vengano presi, se su di una retta, su di un piano o su di uno spazio ad n dimensioni, ovvero, rispetto a quale sistema di coordinate essi vengano riferiti. In teoria, i frattali in questione non sono affatto vincolati ad essere rappresentati su di un piano e possono benissimo essere estrapolati per un qualsiasi numero di dimensioni; il fatto che essi siano solitamente tracciati bidimensionalmente è semplicemente dovuto a comodità di rappresentazione. Ma procediamo con calma! Per i nostri frattali, useremo come formula generatrice la seguente:  Z=z*z+c; chi mastica un po' di analisi si renderà subito conto che si tratta di una parabola traslata rispetto all'origine in base al termine noto c. Quello che interessa a noi tuttavia non è la solita rappresentazione sul piano cartesiano (ovvero secondo un incremento della variabile indipendente), ma come si comporta, dato un punto di partenza, reimpostando nell'equazione i risultati della elaborazione precedente (z=Z) e proseguendo generando una successione di numeri reali il cui comportamento dipende dalla scelta del punto di partenza, nonchè di c. E' proprio questo che genera l'indefinitezza che è una delle caratteristiche peculiari di tali costruzioni matematiche, ovvero la possibilità di iterare virtualmente all'infinito per ciascun punto prima di passare al succesivo. Ecco cosa si intende:

      f(f(f(f(...))))

E' necessario un esempio, perchè gran parte della difficoltà iniziale che si incontra avvicinandosi a questo tipo di frattali viene proprio da questo. Più o meno tutti, nella nostra vita, abbiamo pasticciato un po' battendo a caso i tasti di una calcolatrice tascabile ed abbiamo potuto constatare come, battendo un numero anche molto grande, premendo un certo numero di volte il tasto della radice quadrata, si pervenga sempre al risultato 1 (in realtà vi si giunge anche perchè la precisione di macchina della calcolatrice non può essere infinita). La funzione radice quadrata dunque per ricorrenza si avvicina asintoticamente all'unità. Allo stesso modo, l'elevazione a potenza tende all'infinito impostando un numero >1, a zero impostando un numero <1 e con 1, il risultato rimane costante sull'unità. Dunque, data una condizione di partenza, possiamo analizzare sotto questo aspetto come si comporta, ovvero se tende all'infinito, se tende a zero, o se rimane stabile. Dalla determinazione delle condizioni di partenza, dipendono le differenze fra gli insiemi di Julia e l'insieme di Mandelbrot.

Una vista sul piano complesso

Abbiamo precisato che i frattali vengono usualmente rappresentati su di un piano ed è ora di chiarire un poco meglio la natura e le caratteristiche di esso, nonchè il sistema cartesiano utilizzato come riferimento.
Per fare ciò è necessario presentare alcune informazioni sui numeri immaginari e complessi e come questi ultimi possano essere rappresentati su di un piano. I numeri immaginari e complessi nascono dalla necessità di possedere un qualche modo per esprimere le radici quadrate di numeri negativi, oggetti che non possiedono "diritto di cittadinanza" all'interno di R, l'insieme dei numeri reali.
Per numero immaginario si intende l' unità immaginaria moltiplicata per un coefficente, detto appunto coefficente immaginario. Per unità immaginaria (di solito rappresentata con la lettera i o j), si intende la radice quadrata di -1.
Un binomio formato da un coefficente reale sommato algebricamente ad un numero immaginario forma un binomio complesso che è formato da due parti chiamate appunto parte reale e  parte immaginaria.
Per esempio:
  5+2i
è un numero complesso la cui parte reale è 5 e la cui parte immaginaria è 2.
E' possibile effettuare pressochè qualsiasi tipo di operazione su tali binomi applicando semplici calcoli algebrici.
Per cui:
  (a+bi)+(c+di)=(a+c)+(b+d)i
  (a+bi)(c+di)=ac-bd+(ad+bc)i
dove ovviamente i*i=-1 !
... e via dicendo.

In quanto binomio, ciascun numero complesso può essere considerato come una coppia ordinata, tranquillamente rappresentabile su di un piano cartesiano, previa scelta di un'origine e di unità di misura. Tale rappresentazione ha il nome di piano di Gauss (o di Argand) ed ha interessantissime applicazioni in un sacco di campi differenti della matematica e della fisica che usano in maniera massiccia i numeri complessi, dalla teoria dei circuiti elettronici alla meccanica quantistica.
E' consigliabile raggiungere una buona manualità con i numeri complessi prima di proseguire nell'introduzione: si provi per esempio a calcolare in sequenza le potenze di i, a rappresentare numeri diversi sul piano complesso ed altro. Ogni corso universitario di geometria dedica una parte del programma ai numeri complessi!

Gli insiemi di Julia

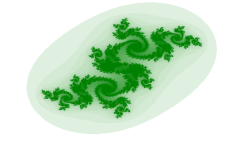
Una vista di un insieme di Julia

Possiamo adesso entrare un poco più in dettaglio ed affrontare i principi di determinazione dei frattali della famiglia di Julia, che si presentano molto diversamente a seconda della scelta del termine noto c.

  1. Si supponga considerare una piccola porzione attorno all'origine di un piano complesso di intervallo (-2,-2)-(2,2).
  2. Si scelga un binomio complesso c assegnando valori del tutto arbitrari alla parte reale ad alla parte immaginaria.
  3. Si sostituiscano, per ogni punto considerato, le corrispondenti coordinate complesse alla variabile z, nell'equazione Z=z*z+c.
  4. Si calcoli il valore di Z.
  5. Se si trova che la distanza di Z dall'origine è maggiore di due, si salti al passo 7. Per calcolare tale distanza, si adotta il teorema di pitagora nel seguente modo: dato Z=a+bi, il quadrato della distanza d dall' origine sarà d2=a2+b2.
  6. Se no, si incrementi di 1 un contatore e si torni al passo 4, se il contatore ha un valore inferiore al numero di iterazioni massime prefissato, dopo aver posto z=Z.
  7. Si colori il punto di un colore diverso a seconda del valore del contatore.
  8. Si azzeri il contatore e si ritorni al passo 3 per calcolare il colore del prossimo punto.
  9. Il procedimento avrà termine quando tutti i punti interessati saranno stati processati in questo modo.
N. B. Il numero di iterazioni massime determina la precisione da adottare per la rappresentazione dell'insieme.
Buoni risultati si ottengono assegnando a c dei coefficenti reali ed immaginari compresi fra -2 e 2.
Vi sono infiniti insiemi di Julia poichè la scelta di c non deve sottostare a nessuna restrizione.

L'insieme di Mandelbrot

L'insieme di Mandelbrot si presenta come un otto disposto in orizzontale sfrangiato e simmetrico rispetto all'asse delle ascisse.

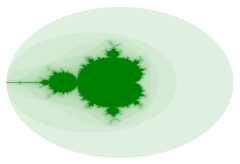
Una vista dell'insieme di Mandelbrot
  1. Si supponga considerare una piccola porzione attorno all'origine di un piano complesso di intervallo (-2,-2)-(2,2).
  2. Si sostituiscano, per ogni punto considerato, le corrispondenti coordinate complesse al termine noto c, nell'equazione Z=z*z+c, ponendo inizialmente z=0+0i.
  3. Si calcoli il valore di Z.
  4. Se si trova che la distanza di Z dall'origine è maggiore di due, si salti al passo 6. Per calcolare tale distanza, si adotta il teorema di pitagora nel seguente modo: dato Z=a+bi, il quadrato della distanza d dall' origine sarà d2=a2+b2.
  5. Se no, si incrementi di 1 un contatore e si torni al passo 3, se il contatore ha un valore inferiore al numero di iterazioni massime prefissato, dopo aver posto z=Z.
  6. Si colori il punto di un colore diverso a seconda del valore del contatore.
  7. Si azzeri il contatore e si ritorni al passo 2, per calcolare il colore del prossimo punto.
  8. Il procedimento avrà termine quando tutti i punti interessati saranno stati processati nel suddetto modo.
N. B. Il numero di iterazioni massime determina la precisione da adottare per la rappresentazione dell'insieme.
La differenza fra l'insieme di Mandelbrot e gli insiemi di Julia è che le coordinate complesse del punto del piano vengono sostituite non a z, inizialmente sempre azzerato, ma a c, che non è più una costante definita all'inizio dell'elaborazione.

Conclusioni

In questo breve intervento, si è voluto dare brevemente alcuni principi utilizzati nei frattali e fornire un metodo pratico per scrivere un programmino capace di disegnare i frattali di Mandelbrot e di Julia.

Se avete un browser che supporta Java, è possibile avere un esempio diretto delle tecniche presentate nella pagina Frattali in Java.

Page log