Isaac Newton
La ricerca dell'infinito e del tutto
NOTE (30 dicembre 2022) - Questo articolo è molto vecchio. Lo scrissi per una conferenzina che feci per un'Università della terza età nella primavera del 2001. Da quanto ho visto nelle statistiche del sito, questa pagina viene ancora visitata (immagino da studenti e studentesse delle scuole superiori). Credo che il contenuto sia sostanzialmente corretto, ma lo stile è un po' ingenuo ed a tratti un po' pesante. All'epoca Wikipedia non esisteva quasi! Nei miei lavori più recenti sono anche molto più preciso sui riferimenti bibliografici. La fonte bibliografica principale è senza dubbio il numero speciale di Le Scienze dedicato allo scienziato e citato in bibliografia come [Guicciardini].Qualche parola sulla situazione storica ai tempi di Isaac Newton
La vita
L'invenzione del calcolo infinitesimale
I fondamenti della meccanica e della gravitazione
I problemi dell'Ottica
Conclusione
Bibliografia
Introduzione
Isaac Newton fu un uomo dal carattere spigoloso ed intransigente, la
cui capacità intellettuale fu tuttavia una delle maggiori di quelle
che mai si furono applicate ai problemi della filosofia naturale. Se Galileo
ebbe il grande merito di introdurre il metodo del pensiero scientifico
moderno e si trovò al centro di una tragica controversia con il
potere ecclesiastico, Newton visse la sua maturità in una liberalissima
Inghilterra anglicana, ove nelle taverne si discuteva di politica senza tema di
repressione ed il potere dello Stato pontificio era ovviamente molto minore
che in Toscana. Lo scienziato applicò la propria innata e stupefacente
abilità in molti campi ed a lui è dovuto forse lo strumento
concettuale forse più potente che l’uomo abbia mai potuto adoperare,
ossia il cosiddetto calcolo infinitesimale. La stessa ideazione del calcolo
trascinò tuttavia lo scienziato ed i suoi allievi in una spiacevolissima
controversia con Leibniz il quale era pervenuto in maniera indipendente
a conclusioni simili; attraverso questi metodi matematici infatti si può
trattare in modo naturale e semplice alcuni aspetti dell’oggetto più
seducente al quale l’uomo abbia mai rivolto il proprio pensiero, ossia
l’infinito.
Qualche parola sulla situazione storica ai tempi di Isaac Newton
La vita di Newton (1642-1727) si svolse in una Inghilterra in pieno fermento intellettuale e politico, in particolare nell’anno della nascita dello scienziato erano in corso aspre battaglie fra il re Carlo I Stuart ed i parlamentari puritani guidati da Oliver Cromwell che si conclusero nel 1648 con la vittoria di questi ultimi e l’inizio della dittatura di Cromwell, in cui ebbero luogo epurazioni dei cattolici irlandesi e scozzesi e nacquero molte sette di ispirazione calvinista. Alla morte di Cromwell tuttavia venne riportata sul trono la dinastia degli Stuart che regnò dal 1660 al 1688 con Carlo II e Giacomo II; quest’ultimo venne poi destituito senza spargimenti di sangue nel 1689 nell’ambito della cosiddetta Glorious Revolution. Dal 1689 in poi il potere parlamentare si rafforzò e l’Inghilterra entrò in un periodo di prosperità economica e di libertà culturale.In Francia si affermò quello stato assoluto retto dai re Luigi XIII e XIV che era stato teorizzato da pensatori come Thomas Hobbes, Jean Bodin e Jacques Bossuet.
Nel 1648 si concluse la Guerra dei trent’anni che aveva funestato l’Europa a partire dal 1618 con l’episodio della defenestrazione di Praga.
La vita
Isaac Newton nacque a Woolsthorpe, nel Lincolnshire il 25 dicembre 1642 (secondo il calendario giuliano) da una famiglia di proprietari terrieri e non conobbe mai il padre, chiamato pure lui Isaac, morto combattendo per il re Carlo I. Giovanotto timido e riservato ebbe un rapporto abbastanza travagliato con la madre Hanna Ayscough Newton la quale alternava periodi di completo abbandono del figlio con altri di attenzioni continue; il giovane Isaac sviluppò pertanto un carattere difficile e nella sua vita fu tormentato da numerosi periodi di profonda depressione e di gravi complessi di inferiorità che lo rendevano estremamente sospettoso con chiunque gli stesse intorno. In particolare, la madre si risposò con un uomo molto più anziano di lei e se ne andò a vivere senza il piccolo quando questi aveva appena un paio d’anni, lasciandolo alle cure della nonna. Questo accadde nel 1645 quando infuriava ovunque la guerra civile fra seguaci del re e seguaci del parlamento. Pure, se ebbe un’infanzia non facilissima e non brillò particolarmente nei primi anni di scuola, la sua vita fu piena di riconoscimenti e di onori, come mai uno scienziato avrebbe potuto aspirare prima di lui.Comunque, il bambino aveva sviluppato un forte attaccamento alla religione, anche grazie alla figura di uno zio, un fratello di sua madre, pastore anglicano, il quale concepiva la guerra civile in termini allegorici contrapponendo la figura del re, visto come un difensore della fede, in contrasto con i parlamentari di matrice puritana. La fede risultò essere un punto fermo di grande importanza per tutta la vita del tormentato studioso, il quale si immerse, specie negli ultimi anni di vita, in approfondite analisi “scientifiche” dei testi sacri in modo da scovarvi segni da interpretare o verità nascoste. Il giovane compì comunque molto in fretta gli studi secondari e giunse nel 1661 presso il Trinity College, che già allora godeva di una grande reputazione in tutta l’Inghilterra; nello stesso anno, veniva rimesso sul trono Carlo II, anche grazie al disfavore prodotto dalle repressive leggi puritane introdotte dopo la vittoria dei parlamentari.
Il giovane dovette tuttavia abbandonare Cambridge per la famosa pestilenza del 1665 (il famoso incendio di Londra è dell’anno successivo) e, rifugiatosi in campagna, si trovò libero di meditare sulle questioni naturali e diede alla luce in questo periodo gran parte delle sue scoperte più brillanti. L’aneddoto della mela cadutagli addosso e che gli avrebbe suggerito la legge di gravitazione universale è apocrifo, ma quello che è certo è che in questo periodo egli si stava interessando al moto di caduta dei corpi ed iniziò a considerare il moto di rivoluzione della luna intorno alla terra come caso limite di un vero e proprio moto di caduta.
Newton entrò ben presto nel corpo docente dell’università di Cambridge ed ebbe una carriera a dir poco fulminante e, come vedremo, ciascuna delle numerose scoperte che fece sarebbe bastata da sola ad assicurargli un posto di rilievo nella storia della scienza. In particolare, nel 1672 il fisico neppure trentenne venne nominato membro della Royal Society di Londra dal re Carlo II e questa era un’onorificenza grandissima, ma la negativa impressione dovuta in massima parte alle critiche di Robert Hooke che suscitarono le teorie relative all’ottica che egli propose turbarono il già difficile carattere di Newton ed egli rassegnò ben presto le proprie dimissioni; si ripropose inoltre di non pubblicare più le proprie ricerche.
In questo periodo tuttavia, si riconciliò finalmente con la madre la quale morì dopo poco tempo.
Intanto, egli divenne un importante professore universitario a Cambridge ed in questi anni egli sviluppò e mise in forma sistematica i fondamentali risultati conseguiti nella giovinezza, da 23 a 25 anni, ma non pubblicò nulla, anche se considerava tempo sprecato qualunque attività che non fosse collegata agli studi che svolgeva negandosi il sonno e dimenticandosi a volte perfino di mangiare. Pare che egli fosse la classica immagine di professore distratto: impegnato nelle sue congetture egli era praticamente inetto ad affrontare qualunque problema pratico riguardante la sua casa o la sua stessa esistenza. In [Gamow] è riportato un curioso aneddoto a lui riferito, ossia che egli praticò un foro nella porta di casa per permettere alla sua gatta di entrare ed uscire a suo piacimento; quando la gatta ebbe dei gattini praticò nella porta ulteriori fori in numero pari a quello dei gattini…
Comunque sia, giunto intorno all’età di 50 anni, nel 1689 egli divenne dapprima deputato nella rappresentanza dell’Università di Cambridge, poi nel 1696 divenne ispettore e successivamente direttore generale della Zecca e si trasferì in veste di alto funzionario a Londra, ove diventò sir nel 1705 e divenne sempre più ricco e coperto di onori; non compì più scoperte fondamentali, ma fu responsabile della condanna al patibolo un buon numero di falsari…
Egli morì il 20 marzo 1727 ed il suo funerale, a cui assistette pure un incredulo Voltaire, si svolse in pompa magna ed Isaac Newton fu inumato nella cattedrale di Westminster accanto alle salme dei grandi d’Inghilterra.
L'invenzione del calcolo infinitesimale
Il contesto culturale matematico del seicento presentava già prima di Newton alcune novità, le quali costituivano un sostanziale passo in avanti rispetto ai mezzi di cui disponeva Galileo; di notevolissima importanza era il lavoro di René Descartes (1596-1650) il quale costituiva un solido ponte fra l’algebra e la geometria, le quali erano prima di lui considerate argomenti della matematica completamente separati e permetteva di trattare con metodi algebrici problemi geometrici e viceversa. Risultati di grande importanza furono quelli ottenuti da John Wallis (1616-1703), il quale, nel suo Arithmetica infinitorum introduceva il concetto di serie infinite; una serie è una somma estesa all’infinito di termini i quali tendono a diventare sempre più piccoli: il punto è che la somma di tali termini può sorprendentemente essere finita.Fin dall’antica Grecia, il concetto di infinito ha meravigliato ed affascinato la mente umana, dimostrando però che la strada che vi giunge è irta di difficoltà e contraddizioni; un esempio di ciò sono i celeberrimi paradossi del moto di Zenone, in particolare quello di Achille e della tartaruga. La situazione è più o meno questa: Achille è dieci volte più veloce della tartaruga, ma parte dieci metri prima di essa; quando Achille riuscirà a superare la tartaruga? Il fatto è che quando Achille avrà percorso dieci metri, la tartaruga ne avrà percorso uno; quando Achille avrà recuperato quel metro, la tartaruga sarà innanzi a lui di dieci centimetri; quando Achille avrà percorso quei dieci centimetri, la tartaruga sarà andata avanti di un centimetro e così via… Il fatto è che la tartaruga rimane comunque sia davanti ad Achille.
Ovviamente, c’è qualcosa che non quadra in tutto il ragionamento, dato che non dubitiamo che prima o poi la tartaruga venga effettivamente superata dal Piè Veloce; ma cosa? Il pensiero greco non fu in grado di comprenderlo.
Eppure l’infinitamente piccolo e l’infinitamente grande compaiono più spesso di quanto si immagini sotto mentite spoglie per poi presentare tutta la loro difficoltà a chi tenti di investigare con maggiore accuratezza sui fenomeni che ci capitano attorno. Prendiamo per esempio il concetto di velocità: essa viene convenzionalmente definita come uno spazio diviso per il tempo impiegato a percorrerlo; se ci pensiamo un attimo, ci accorgiamo che quello che otteniamo è in realtà una media di quello che è il nostro concetto intuitivo di velocità, intesa come un qualcosa caratterizzante il moto di un punto materiale in ciascun istante. Se dividiamo uno spazio 100km per il tempo impiegato da un’autovettura per percorrerlo (poniamo 1 ora) otteniamo la velocità media dell’autovettura nella tratta percorsa, un dato che non ci dice se essa lo abbia percorso effettivamente ad una velocità costante di 100km/h, oppure se essa si sia dovuta fermare ad un semaforo, affrontare delle curve, oppure pagare un casello autostradale ed abbia potuto recuperare il tempo perduto nelle soste con una maggiore velocità di punta nel tragitto. Per migliorare la nostra conoscenza del “come” la nostra automobile abbia percorso i 100km, possiamo pensare di dividere tale intervallo di spazio in due, e fare due misurazioni temporali, in modo da avere due dati di velocità media, che ci danno maggiore informazione. Se non ci bastano due numeretti, possiamo ancora dividere ulteriormente gli intervalli per ottenere 4 velocità medie, 8 velocità medie e così via…
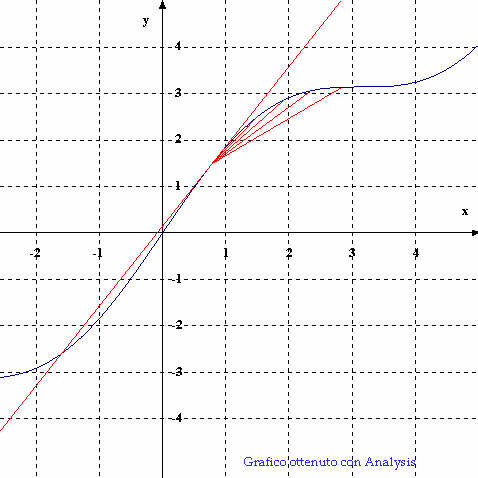
Il problema delle tangenti:
si tratta di calcolare la retta tangente in un punto ad una curva assegnata
(in blu). L’idea è quella di approssimare tale retta costruendo
un insieme di rette (di cui sono rappresentati dei segmenti in rosso),
le quali sono le secanti alla curva in intervalli sempre più piccoli.
Per ricollegarsi con l’esempio del testo, si pensi alla curva come allo
spazio percorso da un’automobile rispetto al tempo; il coefficiente angolare
della retta tangente esprime dunque la velocità istantanea nel punto
di tangenza.
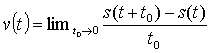
Come si vede, per dare una definizione anche intuitiva di velocità ci troviamo a doverci giostrare con quantità molto piccole, più piccole di qualunque cosa si possa pensare, ma NON nulle… Ecco che ci troviamo a guardare in faccia all’infinito, ma cosa viene fuori dalla nostra formuletta? Dividiamo due quantità sempre più piccole, chi ci dice che il risultato non possa essere nullo, infinito od addirittura non venga fuori proprio nulla? L’aver scritto una formuletta con un passaggio intuitivo ragionevolissimo non ci dà alcuna informazione sulla natura del risultato.
La grande, enorme, fondamentale scoperta di Newton è stata che oggetti come questi si possono trattare in maniera abbastanza semplice con un insieme di regole che egli riuscì a scovare… In particolare, questo tipo di problemi era riconducibile al problema di trovare la tangente ad una curva assegnata.
Tali metodi furono da lui scovati proprio nel periodo di 18 mesi in cui dovette rifugiarsi in campagna per sfuggire alla pestilenza del 1665 e furono da lui chiamate “metodo delle flussioni”, anche se in termini moderni vanno sotto il nome di calcolo differenziale e la velocità istantanea viene detta derivata della legge oraria dello spazio rispetto al tempo. Ma egli affrontò pure il secondo grande problema del calcolo differenziale: quello che abbiamo fatto prima è stato quello di passare dallo spazio alla velocità prendendo il limite di un rapporto, possiamo pensare di effettuare l’operazione inversa e di ricavare invece lo spazio conoscendo l’evoluzione temporale della velocità istantanea; questo è un problema molto più difficile, che va sotto il nome di calcolo integrale e, se non in casi particolari, non è affatto facile “scrivere” la funzione risultante, anche se è possibile provarne l’esistenza. Il problema del calcolo integrale è strettamente collegato a quello di ricavare l’area sottesa da una curva assegnata.
Naturalmente, i metodi introdotti da Newton non erano rigorosissimi e le sue idee (e quelle di Leibnitz) furono messe in un contesto organico da uno sforzo congiunto di molti matematici del XVIII e XIX secolo. Fondamentali, anche in connessione con gli sviluppi del calcolo infinitesimale, furono i suoi studi sulle serie infinite, ossia su somme di infiniti termini i quali diventano via via sempre più piccoli e la sua scoperta della formula dello sviluppo di un binomio.
Una esposizione dei metodi infinitesimali newtoniani fu pubblicata nel Methodus fluxionum et serierum infinitorum, edito postumo in latino nel 1742 e basato sugli inediti accuratamente preparati dallo scienziato.
La fondamentale importanza dell’analisi matematica da lui ideata consiste tuttora nella possibilità di rappresentare fenomeni complessi su scala infinitesimale, con il risultato di avere delle formule relativamente semplici le quali coinvolgono delle quantità e le loro derivate. Questi oggetti matematici sono chiamati equazioni differenziali; per dare un esempio della loro importanza, si pensi che la totalità dei modelli matematici impiegati per descrivere qualunque fenomeno fisico, sia esso l’onda di pressione su di un’ala di un aereo supersonico, sia il calcolo del campo elettromagnetico all’interno di una guida d’onda, viene rappresentato con insiemi di equazioni differenziali le quali possono essere anche in numero di diverse migliaia e per i quali sono state elaborate tecniche efficienti per la risoluzione al calcolatore.
Al calcolo infinitesimale è comunque legato pure un altro illustre nome, quello del tedesco Gottfried Wilhelm Leibnitz (1646-1716), che era una curiosa figura di scienziato-filosofo e che era sostanzialmente un autodidatta nel campo della matematica; egli ideò un metodo sotto certi aspetti analogo a quello di Newton ma, a differenza di quest’ultimo, fece ogni sforzo per rendere pubbliche le proprie scoperte. Leibnitz giunse ai propri risultati in maniera completamente indipendente da Newton e svariati anni dopo le intuizioni del fatidico annus mirabilis 1665 in cui lo scienziato inglese si era rifugiato in campagna e, seppure molto meno rigorosi del calcolo infinitesimale newtoniano, sotto certi aspetti maggiormente simile all’analisi moderna, i metodi di Leibnitz si affermarono molto più in fretta grazie ad una notazione (quella dei differenziali) estremamente efficace e che risultava enormemente più intuitiva e semplice da padroneggiare. Leibnitz infatti fu un grandissimo inventore di notazioni ed è anche grazie a lui che si sono affermati alcuni simboli oggi di uso comune, come l’eguale: “=”, il punto per la moltiplicazione “·” ed i due punti per la divisione “:”.
Nel 1695 Wallis riferì a Newton che in Olanda Leibnitz era considerato l’inventore di un nuovo metodo sotto certi aspetti simile a quello delle flussioni; nel 1699 Nicolas Fatio de Duillier (1664-1753) suggerì durante una relazione presso la Royal Society la possibilità di un plagio delle idee newtoniane da parte di Leibnitz. Quest’ultimo non la prese certo molto bene e nel 1704 rivendicò a sé la priorità della pubblicazione dei metodi infinitesimali accusando a sua volta di plagio la Royal Society londinese; la faccenda degenerò abbastanza in fretta e ne nacque un’astiosa controversia fra i due scienziati ed i loro seguaci e non furono risparmiati colpi bassi, scorrettezze e calunnie. La morte di Leibnitz sopraggiunta nel 1716 pose fine alla questione e Newton ne fu in pratica il vincitore, ma essa provocò una grave frattura fra i matematici inglesi e quelli continentali che perdurò per tutto il XVIII secolo e che fece rimanere l’Inghilterra irrimediabilmente indietro rispetto alla matematica sviluppata nel resto dell’Europa. Questo fu il prezzo delle scorrettezze di Newton nella disputa e fu pagato non da lui, ma da generazioni di matematici che lo seguirono.
Oggi è riconosciuto come diversi scienziati possano arrivare in maniera indipendente a conclusioni simili ed appare ingiustificato il comportamento di Newton che prima non pubblica nulla tenendo per sé le proprie scoperte e poi pretende di avere la priorità su altri studiosi i quali hanno sviluppato intuizioni simili; dobbiamo però riconoscere dapprima la difficoltà di comunicare di Newton dovuta al suo difficilissimo carattere e poi il carattere fondamentalmente differente della scienza del XVII secolo rispetto a quello attuale il quale dovrebbe (anche se a volte non è certo facile) promuovere la comunicazione senza frontiere fra studiosi. Il confronto dialettico infatti non può che essere una fonte importantissima di conoscenza ed è essenziale promuovere gli scambi di opinioni all’interno della comunità scientifica internazionale.
I fondamenti della meccanica e della gravitazione
Se nell'opera di Galileo si potrebbero identificare i principi di quella che in termini moderni verrebbe chiamata cinematica, ossia lo studio del moto di un oggetto a prescindere dalle cause che lo determinano, all'epoca di Newton mancava ancora una comprensione chiara quantitativa proprio di queste ultime, di cosa determinasse il moto e come esse fossero legate al problema cinematico.Newton affrontò questi problemi fin dalla giovinezza e pubblicò l'8 maggio 1686 la prima edizione di un'opera destinata a diventare uno dei testi più importanti della storia della fisica, la cui fama è ancora oggi enorme, forse pari a quella degli Elementi (pubblicati nel III secolo a. C.) di Euclide, od a quella del Dialogo sopra i massimi sistemi del mondo (1632) di Galileo. Quest'opera era intitolata Philosophiae naturalis principia matematica, ossia i principi matematici della filosofia naturale (che a quell'epoca designava quello che oggi chiamiamo scienza); in essa venivano enunciati in maniera chiara e rigorosa i concetti di massa, di quantità di moto, di inerzia e di forza, i quali ancora oggi sono alla base della meccanica e vengono riportati sui libri di testo moderni nè più nè meno nella forma data loro da Newton. La trattazione della meccanica fornita dallo scienziato ingloba ed estende in maniera naturale i risultati di Galileo ottenuti sulla cinematica; egli perviene in sostanza a tre leggi fondamentali le quali vengono chiamate in suo onore leggi di Newton della dinamica che qui riportiamo:
Legge I: ogni oggetto permane nel suo stato di quiete o di moto rettilineo uniforme fintantochè non intervenga una forza a modificare tale stato.
Legge II: La forza necessaria per imprimere ad un dato corpo una determinata accelerazione è legata ad essa attraverso un coefficiente costante che è la massa del corpo.
Legge III: ad ogni azione corrisponde una reazione eguale e contraria o, ciò che è la stessa cosa, le azioni reciprocamente esercitate da un corpo su un altro sono eguali e hanno direzione opposta.
Il lettore non avrà difficoltà nel riconoscere nella Legge I il più famoso dei principi cinematici galileiani; in sostanza esso vuole dire che un qualunque oggetto, se lasciato libero di impedimenti di qualunque genere (attriti, forze di gravità od altro), e se osservato da un sistema di riferimento inerziale o si trova in quiete, oppure si muove di moto rettilineo con velocità rigorosamente costante.
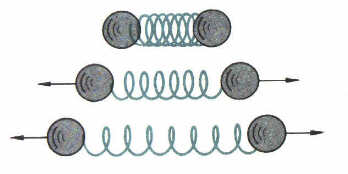 Una rappresentazione della Legge
III data da Gamow: due palline di eguale massa vengono sospinte da una
molla con forza eguale e si muovono pertanto con la medesima velocità
Una rappresentazione della Legge
III data da Gamow: due palline di eguale massa vengono sospinte da una
molla con forza eguale e si muovono pertanto con la medesima velocità
Possiamo pensare di osservare in qualche modo un fenomeno simile guardando un disco da hockey che scivola sul ghiaccio, oppure un carrellino su di una rotaia a cuscino d'aria, insomma qualunque situazione in cui l'attrito è presente in maniera sufficientemente ridotta.
La Legge II lega invece la forza intesa come causa di variazione del moto con l'entità della variazione stessa; in altre parole ci permette di legare l'accelerazione (ossia la variazione della velocità nell'unità di tempo) da noi impressa ad un corpo su cui stiamo agendo con la forza da noi impressa. La Legge II può essere scritta matematicamente con una delle più famose formule della meccanica:
La Legge III (a volte citata a sproposito in argomenti che nulla hanno a che fare con la meccanica) è invece quella che spiega il funzionamento dei motori razzo e di quelli a reazione. Proviamo a pensare ad un asino che trascini un carretto; dal punto di vista dell'asino c'è una forza che gli viene comunicata dal carretto e che lo ostacola nel moto, dal punto di vista del carretto c'è una forza che proviene dall'asino e che lo spinge ad avanzare, la Legge III sancisce che queste due forze sono eguali numericamente, hanno medesima direzione, ma verso opposto. Il motivo per cui l'asino può trascinare il carretto è dovuto all'attrito, infatti gli zoccoli dell'asino esercitano un attrito maggiore sul terreno rispetto alle ruote del carretto che quindi rotolano consentendone l'avanzamento.
Queste leggi sono di fondamentale importanza in quanto consentono di costruire con relativa facilità modelli matematici validi per descrivere praticamente qualunque fenomeno meccanico.
Un'altra grandissima scoperta di Newton che assieme alle leggi esposte sopra lo rende responsabile della definitiva unificazione dei fenomeni celesti con quelli terrestri è la cosiddetta legge di gravitazione universale; essa può essere enunciata come segue: la forza di attrazione gravitazionale fra due corpi è diretta lungo la congiungente dei due ed è direttamente proporzionale al prodotto delle due masse ed inversamente proporzionale alla distanza reciproca elevata al quadrato. L'idea di adottare una legge dipendente dall'inverso dei quadrati non era a dire la verità nuova ai tempi di Newton e sembra che egli fu portato ad adottarla grazie anche alle sue esperienze di ottica avendo osservato che l'intensità della luce proiettata da una candela su uno schermo è proporzionale proprio all'inverso del quadrato della distanza: ad una distanza doppia l'intensità sarà un quarto di quanto si aveva alla distanza iniziale, ad una distanza tripla un nono e così via.
Il merito di Newton sta nell'aver potuto applicare il suo metodo di calcolo infinitesimale a questo problema difficilmente risolubile per altri mezzi dimostrando che le tre leggi di Keplero potevano essere ottenute direttamente dalla sua formula che qui riportiamo:
Le leggi di Keplero furono formulate dal grande astronomo grazie ad ore ed ore di paziente osservazione e di analisi dei dati raccolti da lui e da Tycho Brahe e sono le seguenti:
I. Ogni pianeta si muove su un ellisse di cui il sole occupa uno dei fuochi.
II. Il raggio vettore congiungente il pianeta in esame con il sole spazza aree eguali in tempi eguali.
III. Il quadrato del tempo di rivoluzione planetaria è proporzionale al cubo del semiasse maggiore dell'ellisse descritto.
Il bel passo in avanti sta nell'affermare che la legge di gravitazione universale è valida per qualunque corpo in qualunque situazione: sia esso la Luna che orbita attorno alla Terra, sia una mela che vi cade e che è attratta dal nostro pianeta (si potrebbe dire, grazie alla Legge III che è la Terra ad essere attratta dalla mela). Che differenza dai cieli cristallini ed immutabili difesi dai filosofi in libris che avevano combattuto Galileo e che adesso se ne stavano tranquilli e fiduciosi della loro Verità a dispensarla dai pulpiti e dalle cattedre universitarie pieni della loro boria! Newton con questo passo compì quello che già aveva iniziato Galileo: il rendersi conto che le stesse leggi che valgono sulla terra valgono pure per gli altri oggetti celesti; è questa una delle prime grandi e fondamentali unificazioni della storia della scienza: quella fra i fenomeni terreni e celesti.
Ma perché la Luna non cade sulla Terra, o la Terra stessa non si schianta sul sole? Il motivo è che la Luna possiede una velocità iniziale rispetto alla Terra piuttosto elevata, che le impedisce di precipitarvi sopra, ma è costretta ad orbitarvi attorno indefinitamente in quanto lo spazio vuoto non le oppone nessuna resistenza.
Il sistema solare diventa con l'adozione delle leggi newtoniane però un oggetto abbastanza complicato, in cui ogni pianeta interagisce non solo con il sole, ma anche con tutti gli oggetti celesti, posti a qualunque distanza. Se fu possibile a Newton risolvere il cosiddetto problema dei due corpi, ossia trovare un'espressione analitica che descrivesse il moto di due oggetti dotati di massa interagenti fra di loro, è impossibile effettuare gli stessi calcoli con solo tre corpi e bisogna fare ricorso a tecniche numeriche oggi alla portata di un comune calcolatore da tavolo, ma che hanno frustrato in passato generazioni di valenti matematici. Le leggi di Keplero consistevano dunque solo in un'approssimazione valida grazie alla massa del sole la quale è considerevolmente superiore a quella di tutti gli altri pianeti.
La teoria della gravitazione universale newtoniana permetteva inoltre di descrivere con precisione fenomeni quali la precessione degli equinozi, fenomeno scoperto già da Plutarco e che consisteva nella lenta rotazione dell'asse terrestre attorno al piano dell'eclittica e che si compie con un periodo di 26000 anni, in tutto simile ad un fenomeno analogo osservabile facendo girare una trottola. Un altro fenomeno che veniva così spiegato era quello delle maree, le quali risultavano dall'influenza della Luna e del Sole sugli oceani.
Per dare un'idea della potenza di quella che è la meccanica celeste che costituisce lo sviluppo della teoria newtoniana compiuto da grandi matematici del XVIII e XIX secolo, si pensi che nel 1846 e nel 1930 furono scoperti Nettuno ed Urano, pianeti del sistema solare fino ad allora ignoti, soltanto analizzando le perturbazioni gravitazionali da loro introdotte nei confronti degli altri pianeti osservati.
Al giorno d'oggi abbiamo a disposizione comunque un'altra teoria che descrive gli effetti gravitazionali la cui formulazione matematica è però molto più complessa ma è tuttavia ben più generale; essa è nota con il nome di Relatività Generale e fu sviluppata da Albert Einstein nel 1916 come estensione della sua Relatività Speciale del 1905. Le teorie einsteniane permisero inoltre di eliminare i concetti di tempo e spazio assoluti introdotti da Newton per rendere consistente la propria teoria.
I problemi dell'Ottica
Uno dei campi di grande interesse fin dalla giovinezza fu per Newton lo studio dell'ottica; prima di lui studiosi come Cartesio o Hooke erano giunti a conclusioni teoriche le quali riconducevano i colori a modificazioni della luce bianca considerata semplice. Una leggenda vuole che il giovane avesse acquistato il suo primo prisma nel 1665 presso la fiera di Sturbridge [o Stourbridge] per compiere esperimenti proprio sulla teoria cartesiana dell'ottica.Cartesio infatti pensava alla luce come un fascio di particelle rotanti su sè stesse immerse in una sostanza imponderabile chiamata etere; modificazioni del loro moto di rotazione potevano venire impresse alle sferette e ciò dava luogo ai colori. Come possiamo notare, la spiegazione fornita da Cartesio si inquadra nel tentativo di ridurre ad effetti meccanici pure l'esperienza della visione e rientra bene a far parte di una visione più ampia a cui aspirarono molti filosofi della natura e scienziati fino all'inizio del XX secolo nota sotto il nome di meccanicismo; in essa tutte le leggi naturali relative a qualunque fenomeno potevano essere spiegate con l'effetto di un qualche modello meccanico. E' proprio Newton che, nell'introduzione dei Principia ne traccia una sorta di manifesto: "Mi piacerebbe poter giustificare i fenomeni della natura con i principi della meccanica, poiché ho molte ragioni per sospettare che essi siano basati sull'azione di certe forze, a causa delle quali le particelle, di cui i corpi sono costituiti, per qualche motivo finora sconosciuto, o sono reciprocamente attratte e si raggruppano in forme regolari, o si respingono e si allontanano".
La teoria dell'ottica di Hooke (il quale è tutt'oggi ricordato per i suoi fondamentali lavori sull'elasticità) invece faceva riferimento ad una sorta di "tremore" il quale si propagava in un qualche mezzo e considerava, al pari di Cartesio, come semplice la luce bianca. Newton compì con prismi e lenti tutta una serie di esperienze che lo portarono ad essere convinto della falsità delle teorie sopra riportate ed iniziò dunque a lavorare su ipotesi nuove che verificava tramite esperienze. In questi anni egli sviluppò e costruì quello che è oggi chiamato in suo onore˙ telescopio a riflessione Newtoniano e che è un telescopio costruito con specchi invece che con lenti in modo da eliminare un fastidioso difetto proprio dei rifrattori, ossia che una lente di vetro normale ha un fuoco lievemente differente per i diversi colori dell'iride e ciò porta ad alterare i colori degli oggetti osservati. Con la riflessione un fenomeno simile non avviene e perciò l'aberrazione cromatica (così come viene chiamata questa fastidiosa caratteristica) è totalmente assente, a patto di riuscire a lavorare con sufficiente precisione lo specchio principale (parabolico) in modo da ottenere un'immagine di buona qualità.
Fu proprio per la costruzione del telescopio nel 1668 -l'idea non era proprio originale- che egli fu eletto fellow della prestigiosa Royal Society nel 1672, anno in cui egli pubblica per la prima volta i suoi risultati sulla teoria dei colori. Peraltro, l'accoglienza del suo lavoro non fu delle migliori e fu a causa della controversia che ne nacque con Hooke che egli si dimise dalla Society e decise di non pubblicare nulla; è significativo il fatto che bisognò attendere più di trent'anni per vedere la pubblicazione della prima edizione di un'altra opera fondamentale, ossia Optiks: or, a treatise of˙ the reflections, refractions, inflections and colour of light. Also two treatises of the species and magnitude of curvilinear figures (1704) e che conobbe in tutto tre edizioni, la seconda nel 1706 e la terza nel 1717.
Nell'Optiks è esposta la teoria elaborata dallo scienziato il quale era giunto alla rivoluzionaria intuizione della non semplicità della luce bianca, considerata da lui come la risultante della somma di tutti i colori fondamentali dell'iride; tale posizione gli fu suggerita da una serie di esperimenti in cui fu in grado di dividere un fascio di luce bianca con un prisma per ottenere i vari colori i quali potevano venir rifocalizzati con un sistema di lenti in un fascio nuovamente di colore bianco.
La luce era, in sostanza, composta da un insieme di particelle le quali si muovevano nell'etere, una sostanza imponderabile la quale permeava ogni cosa e poteva essere più o meno denso, senza pertanto presentare resistenza alcuna alla penetrazione dei corpi; la presenza di un gradiente di densità dell'etere era responsabile della deviazione di un raggio luminoso.
La storia del concetto di etere è forse la storia di uno dei più interessanti "falsi indizi" che tormentarono i sonni di non pochi scienziati per poi essere buttato fuori dalle finestre delle aule di fisica da Albert Einstein nel 1905; sostanza impalpabile, tese a ricoprirsi di improbabili proprietà: esso era al contempo leggero e pesante, denso e tuttavia facilissimo da penetrare, poteva in qualche modo contrarsi e poi ritrarsi in modo bizzarro ed altro ancora... Abbastanza per dire che la fisica odierna relativistica non ne sente la mancanza!
L'ottica newtoniana esposta nel 1672 nell'articolo per la Royal Society come abbiamo visto diede˙ luogo ad una polemica piuttosto vivace sulle nuove idee del giovane scienziato; le critiche furono di molti tipi diversi e giunsero in gran parte da coloro che, poco interessati alle regolarità matematiche evidenziate da Newton nelle sue osservazioni, erano più interessati a modelli qualitativi simil-cartesiani composti da sferette ed ingranaggini che descrivessero qualitativamente il comportamento dei raggi luminosi. Posizioni diverse da quelle dello studioso inglese erano inoltre sostenute da Christiaan Huygens (1629-1695) il quale aveva sviluppato un'ottima teoria ondulatoria della luce che spiegava in maniera naturale moltissimi fenomeni di interferenza difficilmente ottenibili con la teoria corpuscolare; Newton è infatti costretto a postulare "ad hoc" delle variazioni e rarefazioni periodiche dell'etere.
Se i fenomeni di diffrazione alla fin fine sembrano suffragare le ipotesi ondulatorie, con l'avvento delle teorie quantistiche all'inizio del XX secolo la luce iniziò a rivelare insospettate caratteristiche corpuscolari; il primo a sospettare tali fenomeni fu nuovamente il geniale Albert Einstein in un articolo pubblicato nel 1905 a fianco di quello sulla Relatività Speciale negli Annalen der Phisik. Il succo è che le caratteristiche ondulatorie e corpuscolari non si mostrano mai assieme ed un modello matematico che ne descrive bene il comportamento in determinate situazioni è stato formulato solo con la meccanica quantistica. Per il lettore interessato, il testo [Feynman] descrive in modo semplice ma rigoroso tale modello.
Conclusione
Come abbiamo visto, la figura di Newton è quella di uno scienziato geniale quanto controverso; in particolare egli sviluppò soprattutto negli anni della maturità un atteggiamento di rifiuto degli studiosi moderni per rifugiarsi nello studio degli Antichi. Egli si dedicò inoltre a studi approfonditi di alchimia e compose numerosi minuziosi commenti a testi sacri ed ad opere alchemiche cercando di applicare allo studio dei testi un metodo "scientifico" simile a quello da lui applicato nello studio della natura. Un idea era di fondo nel suo lavoro di studioso: egli era fermamente convinto del fatto che gli Antichi conoscessero perfettamente la Verità e che la facessero trasparire attraverso messaggi nascosti ed indicazioni ermetiche all'interno dei propri testi; egli pertanto non avrebbe fatto che "riscoprire" leggi già note la cui conoscenza si era poi perduta nel corso dei secoli per l'imperizia dei moderni. All'interno dell'ottica del rifiuto dei pensatori contemporanei, Newton abbandonò i metodi analitici cartesiani i quali avevano avuto una parte determinante nell'ideazione del calcolo per rifugiarsi in metodi geometrici, che erano quelli a disposizione degli Antichi; tutte le dimostrazioni dei Principia sono espresse in questa forma, ormai desueta e pesante per il lettore moderno. Comunque sia, fu anche grazie alla reticenza dei matematici inglesi nell'abbracciare le nuove forme di calcolo analitiche in virtù di un metodo geometrico, "in ottemperanza agli insegnamenti degli antichi" che la matematica inglese rimase, come già accennato, distaccata per quasi un secolo dagli sviluppi che avvenivano nel continente.Le posizioni di Newton, lungi dal poter essere considerate una buona filosofia scientifica, costituivano piuttosto una ingarbugliata miscela di teologia, metafisica ed alchimia, ma avevano se non altro il grandissimo merito di attribuire un'importanza primaria alla matematica nell'investigazione dei fenomeni naturali, posizione non molto comune all'epoca.
Le reticenze dello studioso nel rendere pubblici i suoi lavori erano dovute in parte al suo carattere difficilissimo, in parte alla convinzione che la sapienza dovesse essere patrimonio di pochi eletti, prospettiva che si inquadrava abbastanza con la tradizione alchemica ed ermetica.
Bibliografia
La bibliografia relativa a Newton è, al pari di quella di Galileo, sterminata; mi limito qui a considerare le opere divulgative che trattano le sue scoperte da me utilizzate per la stesura del presente lavoro:[Rossi] Storia della scienza moderna e contemporanea; volume 1: Dalla rivoluzione scientifica all'età dei lumi, tomo 2 , a cura di P. Rossi, Tascabili degli Editori Associati S.p.A. ¸ 1988-1998 UTET
[Gamow] Biografia della fisica di George Gamow, Oscar Saggi Mondadori, settembre 1988; titolo originale: Biography of Physics, Harper Modern Science Series edited by James Newman, 1961
[Guicciardini] Newton: un filosofo della natura e il sistema del mondo di Niccolò Guicciardini edito nella collana "I grandi della scienza" anno 1, n. 2 da Le Scienze, Milano, aprile 1998.
[Guillen] Le cinque equazioni che hanno cambiato il mondo di Michael Guillen, Longanesi & C., febbraio 1998; titolo originale Five Equations That Changed the World, 1995.
[Boyer] Storia della matematica di Carl B. Boyer, Oscar Saggi Monadori, 1990 decima rist. 1998; titolo originale A History of Mathematics, John Wiley & Sons, Inc. 1968.
[Feynman] QED: la strana teoria della luce e della materia di Richard P. Feynman, Adelphi quarta edizione 1996; titolo originale: QED: The Strange Theory of Light and Matter, 1985
[Hoyle] L'astronomia di Fred Hoyle, Sansoni, Firenze 1963; titolo originale
Astronomy, Rathbone Books Limited, London 1962
Log
- December 30, 2022 - Added the page log and the note.
- June 2, 2013 - Correction of typos.
- 2007 - Adapted to the new website.
- 2001 - First version of the page.
