Analysis 2.3
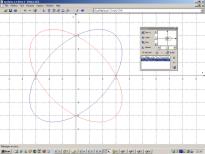
Scarica Analysis 2.3 beta 2 (eseguibili per Windows)
Scarica i sorgenti di Analysis 2.3 (GPL 2.0, scritti in Visual Basic 3.0 e Borland Turbo C++ per Windows 3.1)
Analysis 2.3 è l'ultima versione di un programma su cui ho lavorato per diversi anni. Ho deciso tuttavia di arrestarne lo sviluppo per alcune ragioni. La più importante è che non ho mantenuto neanche un calcolatore su cui sia installato Microsoft Windows. La seconda è che gli strumenti che usai all'epoca per lo sviluppo sono ormai vetusti e tremendamente superati. Il programma viene distribuito gratuitamente, assieme ai suoi sorgenti e sotto i termini della GNU General Public License v. 2.Dapprima concepito come un semplice ausilio per lo studio di funzioni nel triennio della scuola superiore, col tempo ha visto crescere la propria potenza e versatilità fino a diventare un interessante strumento di rapida consultazione anche in ambito universitario.
Per forza limitato come funzionalità (io lavoro da solo, nel tempo libero ed assolutamente gratis!), Analysis è tuttavia facile e veloce da usare, estremamente compatto come spazio occupato, lo si può far funzionare tranquillamente da un dischetto da 1,44 MB, e richiede pochissime risorse di calcolo.
Proprio il suo punto di forza risiede in questo; adattissimo ai primi corsi di Analisi Matematica all'università, consente un rapido controllo degli esercizi svolti senza doversi impratichire con complesse funzioni di programmi più potenti ma più difficili e meno immediati da usare (per esempio Maxima, descritto nella pagina apposita di questo stesso sito).
Ogni comunicazione di qualunque tipo sul programma è sempre benvenuta, anche se sovente non ho tempo di rispondere immediatamente ai messaggi che ricevo.
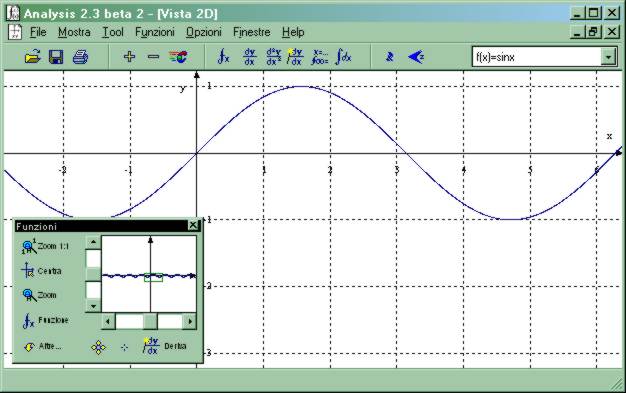
Fig. 1 Ecco
come si presenta la finestra principale di Analysis:
toolbar con i principali
comandi e barra di stato con descrizione delle funzioni
1. Utilizzo di base
1.1 Studio di funzioni della forma y=f(x)
Come già detto, uno degli scopi per cui è disegnato Analysis è lo studio di funzioni. Il programma consente di disegnare oggetti di quattro tipi: funzione bidimensionale del tipo y=f(x), funzione tridimensionale del tipo z=f(x, y), curve parametriche nello spazio del tipo x=x(t), y=y(t), z=z(t) e curve del piano in forma implicita del tipo f(x,y)=g(x,y). Cominciamo con le più semplici: ecco un esempio di funzione bidimensionale (da R ad R): f(x)=sinx
E' da notare come il programma non richieda la presenza delle parentesi per la funzione; esse devono tuttavia essere usate per risolvere problemi di precedenza degli operatori. Un caso in cui le parentesi sono indispensabili è il seguente: f(x)=sin(x*pi) che viene interpretato diversamente da f(x)=sinx*pi.
Tali regole vengono usate per tutte le funzioni primitive fornite da Analysis; vediamo una lista di queste ultime:
Una cosa importante: NON DIMENTICATE I SEGNI DI MOLTIPLICAZIONE; ricevo spesso dei messaggi che dicono cose tipo "Analysis non tratta correttamente la funzione y=4x"; è vero che il programma non dà errore, ma la moltiplicazione deve essere esplicita: y=4*x è la versione corretta.
| + | Somma algebrica |
| - | Sottrazione algebrica |
| * | Prodotto |
| / | Divisione |
| ^ | Elevazione a potenza |
| (...) | Parentesi |
| lg | Logaritmo in base 10 |
| ln | Logaritmo in base e |
| sin | Seno trigonometrico |
| cos | Coseno trigonometrico |
| tan | Tangente trigonometrica |
| sqr | Radice quadrata |
| abs | Valore assoluto |
| arctan | Arcotangente trigonometrica |
| arcsin | Arcoseno trigonometrico |
| arccos | Arcocoseno trigonometrico |
| sinh | Seno iperbolico |
| cosh | Coseno iperbolico |
| tanh | Tangente iperbolica |
| str | Formula di Stirling (approssimazione del fattoriale) |
Di default, è selezionato il grafico bidimensionale ed accanto alla prima riga della finestra c'è la scritta f(x)=, seguita da un campo in cui possiamo introdurre la funzione desiderata; per le prime prove, possiamo scrivere x*x, una parabola molto regolare. Attenzione però! Il programma distingue le lettere maiuscole da quelle minuscole e per lui x e X sono due oggetti distinti. Di questo va tenuto conto soprattutto con le variabili introdotte dall'utente.
A questo punto, dopo aver premuto il pulsante Ok, se tutto è andato bene ci troviamo di fronte alla nostra parabola bella panciuta; se invece c'è stato qualche problema il programma provvede ad evidenziare l'errore ed a comunicare cosa non ha capito (provate ad usare X invece che x per capire cosa intendo).
A questo punto è interessante per esempio sovrapporre al grafico la sua derivata prima, cosa che è possibile fare semplicemente selezionando la voce "Disegna num. derivata I" dal menu "Tool". Se lo facciamo, vediamo sovrapporsi alla parabola una retta inclinata di circa 60° (infatti, la derivata di x*x è 2*x).
Se proviamo poi a cambiare l'espressione della parabola, per esempio introducendo y=3*x^2, vedremo che automaticamente la derivata numerica si adatterà ai cambiamenti appena effettuati.
1.2 Calcolo analitico della derivata
Nell'Analisi matematica, una delle operazioni più importanti che ci si trova a svolgere su di una funzione è senza dubbio la derivazione (parziale o totale) rispetto ad una variabile, nella grande maggioranza dei casi la x. Se la funzione di partenza è derivabile (è richiesta, fra le altre cose, la continuità), la derivata fornisce numerose informazioni utili, in particolare la posizione degli estremi relativi (massimi o minimi), nonchè flessi a tangente orizzontale.Rispetto all'integrazione indefinita, che può essere vista come l'operazione inversa della derivazione, esistono semplici regole che, applicate in maniera meccanica all'espressione di partenza, forniscono quanto cercato a meno di errori di calcolo i quali spesso "sfuggono" nel fare i conti a mano. Poichè la derivazione non è un compito che richieda alcuna facoltà intellettuale, a meno di applicare bene le formule, è un compito estremamente adatto ad essere eseguito con un calcolatore. Ciò ovviamente non vuol dire che non si debba imparare a fare i calcoli a mano! Il computer può tuttavia fornire un utile mezzo di confronto (sempre se il programma non contiene degli errori)
Per far derivare analiticamente una funzione ad Analysis basta fare click sulla voce "Derivazione analitica" del menu Tool; si perviene ad una finestra nella quale si può introdurre la funzione da derivare (oppure sceglierla dalla lista delle funzioni già impostate per il disegno) ed il simbolo rispetto al quale derivare. La derivazione avviene in due fasi distinte: nella prima si applicano in maniera cieca le regole di derivazione nella loro forma più generale possibile ottenendo tuttavia un'espressione che, seppure corretta, risulta di lettura molto poco agevole; nella seconda si semplifica la derivata testè trovata, per ottenerne una forma analitica di più agevole lettura, rimuovendo le parentesi non necessarie, moltiplicazioni per zero, ecc... C'è una cosa importante da notare ed è che un'espressione come la seguente:
La derivazione analitica (che fornisce l'espressione della derivata) è rappresentata con il simbolo di derivazione di Leibnitz dy/dx contraddistinto però da una "bacchetta magica", per differenziarla dalla derivazione numerica, presente anche nelle vecchie versioni di Analysis che consente di calcolare il valore assunto dalla derivata solo per punti. La derivata (prima e seconda) calcolata per punti era disponibile fin dalla prima versione di Analysis ed è stata mantenuta per compatibilità e per essere usata ove non interessi avere un'espressione analitica della derivata in questione.
N.B. il derivatore ed il semplificatore funzionano ragionevolmente bene nel senso che forniscono un'espressione che dovrebbe essere corretta, sia pure in forma non usuale. Possono tuttavia sussistere ancora errori ed il modo migliore per verificare se il derivatore analitico ha fornito la risposta corretta è quello di confrontare i grafici con quelli forniti dalla derivazione numerica. In caso di errore, non esitate a scrivermi per segnalarmi la situazione anomala (specificate in particolare la funzione che la provoca).
1.3 Impostazioni di zoom
Lo zoom è l'operazione di ingrandimento di particolari del grafico; Analysis dispone di due meccanismi differenti per ingrandire un'area.Il primo, più immediato, consiste nel cliccare e trascinare all'interno della finestra Vista 2D il puntatore del mouse attorno al particolare che si vuole ingrandire: al rilascio del pulsante, l'area selezionata viene automaticamente scalata fino a riempire l'intera finestra. Attenzione però che non vengono conservate le proporzioni!
Il secondo metodo invece è più versatile e consiste nell'accedere ad una finestra apposita tramite la voce "Imposta zoom" del solito menu "Tool". In questa finestra, visibile in figura 3, sono presenti numerose opzioni:
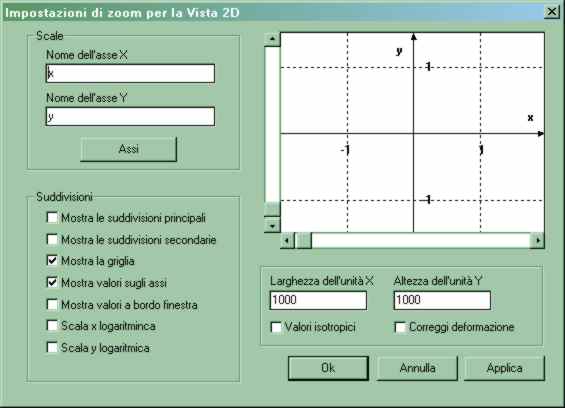
Fig.
2: la finestra di impostazione dello zoom
Le due linee di teso consentono di dare un
nome differente agli assi, invece dei soliti x ed y, per
l'ingrandimento sono essenziali le barre di scorrimento visibili ai lati
dell'anteprima ed i due campi di testo sotto di essa.
Provando a muovere le barre di scorrimento, le unità di
misura orizzontali e verticali vengono dilatate o ridotte ed i valori
mostrati nei due campi variano di conseguenza. I numeri sono una misura
della dimensione delle unità; il valore 1000 assunto come default
rappresenta una lunghezza di circa tre centimetri in un monitor da 15 pollici.
Il fattore di zoom può variare in un intervallo piuttosto ampio
ma per esigenze estreme esso può venir ulteriormente ampliato cliccando
sul bottone "Assi". Esso consente di impostare il valore numerico associato
ad un'unità di misura e può variare considerevolmente (circa
600 ordini di grandezza, e scusate se è poco); inoltre possono essere
impostati fattori particolarmente asimmetrici.
Le opzioni visibili sulla sinistra consentono di modificare l'aspetto
degli assi; provate a selezionarle e guardatene l'effetto nell'anteprima.
In qualunque momento, è possibile tornare allo zoom 1000x1000
e centrare il grafico selezionando la voce "Zoom 1:1" del menu "Tool".
Una novità della versione 2.2 è la possibilità
di ritornare molto rapidamente alla visualizzazione precedente semplicemente
selezionando "Zoom precedente" dal menu "Tool", questo consente di ingrandire
un particolare per ritornare rapidamente alla visione di insieme che
si possedeva in precedenza. Tale funzione è attuabile anche premendo
la freccina azzurra visibile nella Toolbar sotto la barra del titolo
ed i menu.
1.4 Scorciatoie e trucchi
Per rendere più rapido ed immediato l'utilizzo del programma, fin dalla versione 2.0 ho introdotto una barra sotto i menu che riporta i principali comandi usati più di frequente. Essa si presenta, un po' come nei programmi più recenti, con un aspetto piatto ed i pulsanti si alzano al passaggio del mouse. Inoltre in basso viene riportata una sintetica descrizione del comando azionato dal bottone su cui si trova il mouse; questo avviene anche con le voci dei menu per rendere più chiare le funzioni svolte da ciascun comando.A proposito, sono ben accetti eventuali suggerimenti e critiche riguardo l'usabilità del programma; certe cose per me ovvie possono non esserlo per chi ha appena scaricato Analysis e sta provando ad usarlo per le prime volte.
Altro strumento molto utile è una finestrina dal solito aspetto piatto che contiene altre scorciatoie per comandi quali lo zoom, la centratura automatica del grafico bidimensionale nella sua finestra, la lista delle funzioni presenti in memoria, l'impostazione della funzione corrente e la possibilità di far scorrere il grafico a destra, a sinistra, in alto ed in basso.
Per attivare questa finestra, visibile in figura 4, è necessario attivare la voce "ToolWindow" del menu "Mostra"; come potete notare, tale finestra è predisposta in modo da essere sempre in primo piano in modo da potervi accedere in ogni momento.
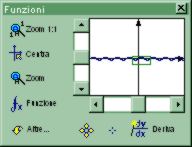
Fig.
3: la ToolWindow
La "croce" visibile nel rettangolo bianco sopra
le barre di scorrimento rappresenta gli assi cartesiani visti in un estensione
variabile intorno all'origine e l'area del grafico bidimensionale nella
finestra Vista 2D è rappresentata con un rettangolo verde sopra una
riproduzione del grafico in esame visto con uno zoom piuittosto ampio. Così,
in ogni momento sappiamo dove stiamo guardando! Sotto il rettangolo, a fianco
del bottone di derivazione analitica sono presenti due pulsanti i quali consentono
di aumentare o ridurre la porzione del grafico mostrata attorno agli assi.
Il pulsante "Altre" mostra la lista delle funzioni in memoria e altri comandi
per aggiungerne, eliminarne ed impostarne il colore.
Vi è poi un'altra scorciatoia importante: provate a fare
click con il pulsante destro del mouse in mezzo ad un grafico bi e tridimensionale;
vi apparirà un menu a tendina contenente le operazioni più
frequenti per quel tipo di grafico!
1.5 Curve in forma implicita
La possibilità di rappresentare curve piane espresse in forma implicita, ossia oggetti specificati attraverso l'eguaglianza di due funzioni, ossia f(x,y)=g(x,y) è la principale novità della nuova versione 2.3 di Analysis. Attraverso le nuove potenzialità messe a disposizione dal programma, è facile disegnare una circonferenza in forma implicita semplicemente scrivendo x^2+y^2=9 all'interno della finestra "Impostazione funzione" (a cui si accede dal menu "Tool") dopo aver selezionato "Curve in forma implicita" all'interno della lista di possibili oggetti rappresentabili.Lavorare con questo tipo di funzioni è in tutto e per tutto simile al modo di operare già visto in 1.1 per quanto riguardava le classiche funzioni bidimensionali y=f(x). Tuttavia, poichè il programma applica delle tecniche di approssimazione per disegnare la curva e non tenta in alcun modo di esplicitarla, molte delle tecniche che erano disponibili, come la derivazione analitica od i metodi numerici per la ricerca di zeri o massimi e minimi non possono essere utilizzate.
La possibilità di rappresentare curve f(x,y)=g(x,y) consente di ampliare di molto la classe di oggetti trattabili con Analysis che così può essere utilizzato anche per la didattica della geometria analitica.
2.Utilizzo avanzato
2.1 Le funzioni R2->R
Tecnicamente, una funzione tridimensionale non è molto diversa da una funzione di una sola variabile. L'unica differenza è che ha bisogno di due numeretti in ingresso, per esempio x ed y, per calcolarne un terzo, la z appunto; Analysis si basa proprio su questo per calcolare i grafici tridimensionali che può rappresentare con diverse viste prospettiche.
Per le nostre prime prove, possiamo partire da una funzione molto semplice: f(x, y)=x*x+2*y*y, che è un paraboloide un po' più panciuto nella direzione dell'asse delle y.
Per introdurre l'espressione nel programma si segue ne più ne meno la stessa trafila già vista per le "solite" funzioni y=f(x) attraverso la voce "Imposta funzione" del menu "Tool" con l'unica differenza che è necessario selezionare la voce "Tridimensionale" nell'area "Tipo funzione".
Dopodichè potremo digitare quanto segue il simbolo di uguale, ossia x*x+2*y*y nel campo di introduzione del testo della funzione. A proposito, notate che a fianco del campo la scritta f(x)= è diventata f(x, y)=, per ricordarci che abbiamo a che fare con un oggetto a due variabili.
Fatto questo, premiamo Ok e se tutto è andato bene ci troviamo di fronte il nostro paraboloide piuttosto allargato (notate la scala sull'asse delle z). Questo perchè l'area standard di visualizzazione (x, y) è un reticolo di 40x40 intorno all' origine ed i quadrati crescono piuttosto rapidamente; per modificare tale area, accediamo alla finestra di impostazione del grafico tridimensionale dalla voce "Caratteristiche Vista 3D" nel menu "Mostra".
All'interno del riquadro "Intervallo rappresentato", introduciamo i valori seguenti:
x y zL'opzione "adatta z" deve rimanere selezionata e così il programma provvederà da solo a calcolare gli estremi in z che gli saranno maggiormente convenienti.
Alto sin. -2 2 ---
Bas. des. 2 -2 ---
Selezionando il tasto Ok citroviamo di fronte ad un qualcosa di più rassicurante.
Cerchiamo un po' di capire cosa abbiamo fatto: i valori introdotti corrispondono alle coordinate dell'angolo in alto a sinistra ed in basso a destra dello schermo ed in particolare l'intervallo delle z ci consente di vedere tutto il paraboloide che abbiamo introdotto.
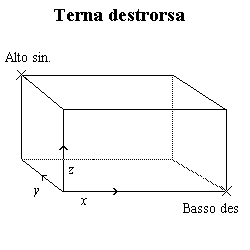
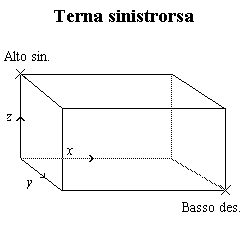
Fig.4: la
posizione degli angoli e degli assi in terne destrorse e sinistrorse
Questi numeri rappresentano l'equivalente
nel grafico tridimensionale dell'impostazione di zoom descritta per le funzioni
di una variabile.
Vale la pena di spendere due parole sulle terne cartesiane, esistono
infatti due modi di comporre tre rette orientate ed Analysis li permette
entrambi. Il caso più frequente è quello delle terne destrorse,
così dette perchè seguono la cosiddetta regola della mano
destra: fatti corrispondere l'asse x alle dita di una mano destra
distesa e l'asse y al palmo, il pollice indica la direzione dell'asse
z. Questa regoletta mnemonica, che non è altro che
una convenzione per raccapezzarsi con i prodotti vettoriali, è anche
detta regola della scimmia per le posizioni assurde in cui
chiunque finisce inevitabilmente per mettersi all'atto di applicarla.
Le terne sinistrorse si ottengono da quelle destrorse semplicemente
invertendo la punta di uno degli assi; nella figura 4 ho invertito l'asse
delle y.
Come dicevo, Analysis supporta i due tipi di grafico ma normalmente
è impostato per visualizzare una terna destra; per visualizzarne
una sinistra potete selezionare l'opzione "Terna sinistrorsa" nelle "Opzioni
di visualizzazione" all'interno della finestra da cui avete impostato lo
zoom.
Ma al di là delle questioni tecniche il risultato è visibile
in figura 4.
Un problema delle vecchie versioni di Analysis era la difficoltà
di scegliere correttamente gli intervalli di visualizzazione, in modo che
la superficie da tracciare venisse disegnata senza essere ridotta troppo,
oppure senza essere "esplosa" molto al di fuori dalla porzione rappresentabile
sullo schermo. Dalla versione 2.2, si possono specificare solo gli intervalli
x ed y (gli estremi vanno introdotti in qualsiasi ordine,
penserà il programma ad ordinarli in modo corretto) e richiedere
ad Analysis di calcolare automaticamente la porzione di z da visualizzare.
A volte tuttavia le scelte di Analysis non sono proprio ottimali ed
è sempre possibile modificare gli estremi calcolati dal programma
in maniera automatica, i quali costituiscono sempre un utile punto di partenza.
Ricordate che il massimo valore introducibile come estremo di
visualizzazione (x, y od z) è limitato a 100,
tuttavia è possibile espandere notevolissimamente tale limite scegliendo
appropriatamente (esattamente come nei grafici 2D) l'unità di misura
più appropriata per ciascun asse.
2.2 I colori nei grafici 3D
Ci vuole un po' di colore nella vita... Analysis segue questa filosofia mettendo a disposizione diversi modi per colorare un grafico tridimensionale; dalla colorazione in tinta unita, alle mappe di colore, al wireframe, il tutto per rendere più chiaro ed accattivante un grafico 3D.Per accedere alle varie opzioni di colorazione, è necessario che sia stata impostata e selezionata come corrente una funzione tridimensionale; per semplicità mi rifarò all'esempio del paraboloide introdotto nel paragrafo precedente. A questo punto, basta selezionare la voce "Colore" del menu "Funzioni" per accedere ad una finestra (mostrata in figura 6) che permette di scegliere le principali modalità di colorazione.

Fig.5: ecco
come si presenta una mappa di colore nei grafici
Per rappresentare una superficie tridimensionale,
il programma la approssima con tanti quadrilateri che vengono modellati
in modo da adattarsi al meglio alla conformazione originale. Ciascun poligono
è composto da un bordo (i quattro segmenti che racchiudono il quadrilatero)
e da una parte interna racchiusa da esso. La parte interna può essere
colorata in due modi diversi o non essere colorata affatto, infatti, a
ciascun poligono può venire assegnato un colore unico, oppure un
colore differente scelto da una mappa a seconda del valore medio di z
che gli compete. Questo secondo metodo di colorazione offre anche i risultati
più accattivanti, ed attraverso mappe di colore (molte sono distribuite
con il programma, provatele) potete sfruttare al meglio la modalità
di visualizzazione "dall'alto" che avrebbe poco senso con colorazioni a tinta
unita; infatti, tale combinazione è probabilmente la migliore da usare
con grafici particolarmente complessi. La mappa colore viene specificata
con il nome del relativo file che deve essere specificato nell'apposito riquadro;
attraverso il bottone "Sfoglia" potete accedere ad una finestra di dialogo
standard per il caricamento dei file. Provate a vedere con il pulsante "Mostra
>>" i risultati dei cambiamenti, è facile rendersi conto di
come funziona l'intera struttura.
Una mappa è sostanzialmente un insieme di colori specificati
secondo lo standard RGB con tre valori da 0 a 255 rispettivamente per il
rosso, il verde ed il blu in ogni riga del file; questo insieme di colori
viene ripartito con legge lineare fra il valore minimo ed il valore massimo
di z impostati. Anche qui è possibile richiedere al programma
di calcolare il valore minimo e massimo assunti dalla funzione nell'intervallo
specificato per adattare in maniera automatica gli estremi della mappa colore
alla superficie in esame.
La voce "Wireframe" che si potrebbe tradurre in qualche modo con "struttura
a fili" non colora l'interno dei poligoni che così rimangono trasparenti;
resta inteso che in questo caso la voce "Disegna contorno poligoni" deve
essere selezionata, altrimenti non vedrete assolutamente nulla...
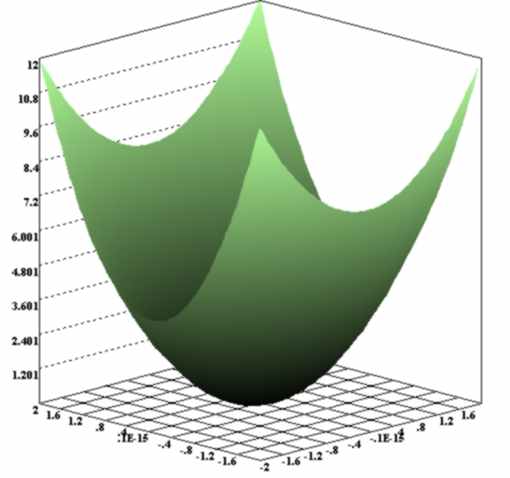
Fig.6: Il
paraboloide descritto nel testo, con una mappa di colore.
Per questo, una delle novità della versione 2.2 è la possibilità di adottare lo shading di Gouraud nel disegno dei poligoni: il punto chiave è che ogni poligono viene riempito con un colore non uniforme e cangiante da punto a punto, in modo da interpolare linearmente quello calcolato ai quattro vertici. Ciò permette di mascherare notevolissimamente il passaggio da un poligono all'altro, consentendo di migliorare molto la resa, soprattutto se sono disponibili un buon numero di colori. Lo shading di Gouraud ovviamente allunga il tempo necessario per disegnare ogni singolo poligono, ma consente di ridurne di molto il numero complessivo per ottenere risultati di buona qualità. La procedura di shading si attiva selezionando la voce corrispondente nella finestra che permette di definire il colore di un grafico 3D. Associata all'opzione di shading, v'è lo Z-Buffering, il quale consente (a prezzo di una maggiore occupazione di memoria) di gestire in maniera molto precisa intersezioni fra differenti superfici.

Fig 7: Immagine
ottenuta con il flat shading con un basso numero di poligoni

Fig.8: Immagine
ottenuta con lo shading di Gouraud disegnando i medesimi poligoni della
precedente
Per una migliore resa estetica, provate a
selezionare le varie viste prospettiche per vedere quali rendono meglio e
provate a selezionare le varie "Opzioni di visualizzazione" nella finestra
"Imposta Vista 3D".
Di queste ultime, in particolare vanno segnalate "Sfondo nero" che
spesso rende più belli i grafici e "Non deformare gli assi" che
consente di mantenere fissate le proporzioni di un disegno anche ridimensionando
la finestra.
2.3 Funzioni parametriche
A partire dalla versione 2.2, Analysis mette a disposizione la possibilità di disegnare dei grafici di funzioni parametriche del tipo x=f(t); y=g(t); z=h(t) che vengono tracciate nello spazio (x, y, z) seguendo le stesse identiche regole viste sopra per le funzioni tridimensionali. Nella terminologia di Analysis tali oggetti vengono spesso chiamati "Traiettorie" per l'ovvia interpretazione fisica legata al moto di un punto nello spazio.Attraverso tale tipo di visualizzazioni, è interessante osservare quelle che sono chiamate "figure di Lissajous" che tradizionalmente si osservano con l'oscilloscopio introducendo negli ingressi X ed Y segnali sinusoidali con frequenza e fase differente.
Un esempio potrebbe essere il seguente; selezionate la voce "Imposta Funzione" dal menu "Tool" e, nella finestra che comparirà, già vista al paragrafo 1.1, selezionate "Parametrica x=f(t); y=g(t); z=h(t)". Oltre la prima riga dove avevamo introdotto le funzioni nei paragrafi 1.2 e 2.1, ne verranno abilitate una seconda ed una terza; in esse scrivete t, sint e cost in modo da impostare due sinusoidi sfasate dell'angolo retto. Premuto il pulsante Ok, vedrete comparire un'elica nel grafico tridimensionale che rappresenta le tre espressioni introdotte. Figure più complesse si osservano variando la fase e l'ampiezza di una sinusoide e lasciando invariata l'altra, oppure usando funzioni iperboliche.
Naturalmente, è necessario specificare un opportuno intervallo all'interno del quale il parametro t possa convenientemente variare; questo lo si specifica all'interno della stessa finestra dalla quale si era impostata la funzione di partenza, avendo cura di introdurre valori significativi in modo che l'intervallo di variabilità non sia eccessivo (questo giocherebbe a discapito della precisione del disegno del grafico).
2.4 Un esempio "fisico"
Per chi non ha molta dimestichezza con funzioni trigonometriche, ed amenità varie, ecco un esempio che dovrebbe chiarire un po' meglio le cose riguardante una semplice situazione cinematica.Immaginate un cannone con bocca orizzontale che spari un proiettile con velocità di 10m/s sull'orlo di un profondo dirupo; con un sistema di riferimento posizionato come in figura 8, vogliamo capire quale sarà la traiettoria del problema trascurando l'attrito dell'aria ed ogni effetto dissipativo, in modo da concentrarci solo sull'aspetto cinematico della questione.
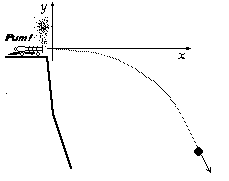
Fig. 9: Il
sistema di riferimento scelto
Per la semplicità del sistema, possiamo analizzare il sistema ricavando le equazioni del moto separatamente per i due assi per poi metterle assieme con Analysis; infatti lungo l'asse x la velocità non varia e dunque lo spazio percorso dall'origine è dato da:
Nell'asse z rappresentiamo lo scorrere del tempo, e perciò:
Analysis mostrerà una parabola con la concavità rivolta verso il basso vista in prospettiva che è infatti il risultato della composizione dei due moti. Per tale tipo di problemi ove non interessa mostrare il parametro t nel grafico, potete selezionare la vista "Superiore" nelle impostazioni del grafico 3D e la vostra parabola vi comparirà in tutto il suo splendore.
2.4 Note per chi abbia usato versioni precedenti
La modalità di visualizzazione delle funzioni parametriche è cambiata in maniera piuttosto notevole dalla versione 2.1 del programma, file creati da vecchie versioni potrebbero pertanto non essere visualizzati in maniera eguale dalla versione 2.3 a causa dell'introduzione dell'intervallo di variabilità del parametro che va obbligatoriamente impostato, nonchè a causa di una differente disposizione degli assi che sono stati uniformati alla scelta effettuata nei grafici di superfici tridimensionali.Vedere le funzioni esattamente come apparivano in Analysis 2.1 basta scambiare l'espressione corrispondente ad x con quella relativa alla z, ed impostare un opportuno intervallo di variabilità di t.
3. Altre informazioni
3.1 Problemi riscontrabili
Ed ora veniamo alle dolenti note... Le vecchie versioni di Analysis contenevano parecchi errori ed erano affette da molti problemi che spesso terminavano con un drastico "Square root of a negative number" anche per operazioni assolutamente non correlate con l'estrazione di una radice quadrata. Il motivo di questo problema è piuttosto tecnico ed è connesso con gli interrupt hardware del coprocessore matematico che non venivano gestiti correttamente e portavano in crash la macchina; le librerie non venivano scaricate correttamente e l'unica soluzione era un reset della macchina.Se scovate un comportamento anomalo del programma che si sviluppa in condizioni ripetibili (ossia sempre o spesso dopo aver commesso determinate operazioni) non esitate a comunicarmelo; la maggior parte dei problemi sono banali e sono risolubili in pochi minuti in modo da rilasciare versioni sempre migliori del programma. Gran parte degli errori che ho avuto occasione di correggere fino ad adesso sono connessi con la parte "di interfaccia" con l'utente in modo che il programma non andasse in palla per degli errori nell'introduzione dei dati o cose del genere.
Non è certo una scusa, ma pensate quante volte vi è impazzito Word!
Un altro aspetto che può presentare errori è il supporto multilingue: se avete voglia e tempo e conoscete bene una delle lingue disponibili, potete usare il programma in tale lingua e segnalarmi eventuali errori di scrittura presenti.
Naturalmente, proposte di traduzione in altre lingue (per esempio lo spagnolo ed il tedesco) sono accette molto volentieri!
3.2 Caratteristiche tecniche
| Sistema operativo richiesto | Windows 3.1 o superiore |
| Processore richiesto | Pentium 100MHz |
| Occupazione su disco | 1,3 MB |
| Richieste particolari | Nessuna |
3.3 Installazione del programma
Analysis 2.3 possiede una procedura di installazione semplice e funzionale; dopo aver scaricato il file EXE da Internet è infatti sufficiente eseguirlo e seguire a video i pochi passi necessari come qualunque altro programma per Windows.3.4 Sapete usare bene Analysis?
E' da un po' di tempo che usate Analysis? Trovate che alcuni punti della documentazione non siano molto chiari? Volete proporre qualcosa di aggiuntivo o descrivere tecniche che avete sviluppato sul programma per eseguire calcoli particolari? Se volete scrivere un articolo, una breve relazione da pubblicare sul sito, o soltanto dare un semplice suggerimento, scrivete a: davbucciEVITALOSPAM@tiscalinet.it
License:
--------
Copyright (C) 2007 Davide Bucci davbucci at tiscali dot it
This program is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program; if not, write to the Free Software
Foundation, Inc., 675 Mass Ave, Cambridge, MA 02139, USA.
