Introduction à Gnuplot
Un logiciel libre dédié aux graphiques scientifiques
Quelques idées pour commencer
Comment tracer une fonction
Graphiques à partir d'un fichier
Un exemple de lissage de données expérimentales
Obtenir un graphique en Postscript
Représentation avancée de surfaces
Conclusion
Introduction
Gnuplot est un logiciel utile pour tracer graphiques de toutes les formes. S'il est utilisé correctement, il peut fournir des résultats très professionnels, souvent bien supérieurs à ceux que l'on peut obtenir avec Excel, par exemple. Exactement comme Maxima, il s'agit d'un logiciel qui existe depuis beaucoup de temps (1986, pour la précision) et il est complètement multi plateforme. Ceci est un avantage non négligeable... Dans mon travail, je me suis retrouvé à passer continûment entre Windows, Linux et MacOSX : depuis plusieurs années, j'essaye d'utiliser des logiciels qui ne me contraignent pas à utiliser un système d'exploitation en particulier. Une difficulté majeure de Gnuplot est le fait qu'il s'agit d'un logiciel interactif à ligne de commande qui peut être utilisé à partir du terminal. Les premières fois, il semble suivre une logique difficile à saisir, d'où la présence de cette petite page, afin de commencer à se faire une idée sur les possibilités de ce logiciel.
Cette page a été écrite sur la base de plusieurs interventions que j'ai faites sur le forum en italien de Macitynet, où je participe souvent avec le pseudonyme de DarwinNE :
Comme j'ai fait pour Maxima, j'évite de décrire en détail chaque commande (pour cela, il suffit de taper help, suivi de la commande dont on cherche les détails). Je préfère fournir par contre des exemples concrets, qui peuvent être utiles pour bien comprendre la philosophie qui est utilisée par le logiciel.
Quelques idées pour commencer
La première chose dont il faut se rendre compte est que Gnuplot ne dessine pas directement sur l'écran ou sur une fenêtre, mais plutôt dialogue avec un *terminal* graphique. Ce dernier est un module logiciel qui a pour but de mettre à disposition un certain nombre de fonctions graphiques de base, qui sont utilisées ensuite par Gnuplot. En vertu de l'importance centrale du terminal, Gnuplot au démarrage nous fournit quelques informations sur sa version et spécifie le terminal qui est utilisé :
[davidebucci@davide-bucci-portable]$ gnuplot
G N U P L O T
Version 4.2 patchlevel 0
last modified March 2007
System: Darwin 8.10.1
Copyright (C) 1986 - 1993, 1998, 2004, 2007
Thomas Williams, Colin Kelley and many others
Type `help` to access the on-line reference manual.
The gnuplot FAQ is available from
http://www.gnuplot.info/faq/
Send comments and help requests to <gnuplot-info@lists.sourceforge.net>
Send bug reports and suggestions to <gnuplot-bugs@lists.sourceforge.net>
Terminal type set to 'aqua'
gnuplot>
Pour terminer la session, il suffit de donner la commande quit :
gnuplot> quit [davidebucci@davide-bucci-portable]$
La version de Gnuplot que je suis en train d'utiliser est la 4.2 (plutôt récente, du moins dans le moment où j'écris ce texte). Le terminal utilisé s'appelle Aquaterm et fonctionne très bien sous MacOSX et que l'on peut trouver sur VersionTracker et installer de façon indépendante. Si vous utilisez Linux ou Windows, vous trouverez probablement les terminaux x11 ou Windows à la place d'Aquaterm. MacOSX peut aussi utiliser le terminal x11, mais il n'y a aucune raison de faire cela, car Aquaterm fonctionne très bien et il est très léger.
Pour obtenir une liste de terminaux disponibles, par curiosité, il suffit de taper set terminal et ensuite retour. Il faut faire très attention au fait que Gnuplot distingue la casse des commandes qui sont insérées : SeT TeRmInAl ne va pas fonctionner, de la même façon que SET TERMINAL.
gnuplot> set terminal
Available terminal types:
aqua Interface to graphics terminal server for Mac OS X
dumb ascii art for anything that prints text
emf Enhanced Metafile format
emtex LaTeX picture environment with emTeX specials
epslatex LaTeX picture environment using graphicx package
fig FIG graphics language for XFIG graphics editor
gif GIF images using libgd and TrueType fonts
jpeg JPEG images using libgd and TrueType fonts
latex LaTeX picture environment
mf Metafont plotting standard
png PNG images using libgd and TrueType fonts
postscript PostScript graphics, including EPSF embedded files (*.eps)
svg W3C Scalable Vector Graphics driver
x11 X11 Window System
gnuplot>
Dans l'exemple que l'on vient de fournir, en réalité la liste était beaucoup plus longue, mais je l'ai raccourcie un peu, en me limitant aux terminaux les plus intéressants. Nous allons voir quelques exemples dans la suite de notre discussion. On peut aussi se trouver dans la situation où, dans des installations incomplètes par exemple, Gnuplot n'ait pas un terminal défini par défaut. Dans ce cas, au démarrage, on aura quelque chose du style :
Terminal type set to 'unknown' gnuplot>
Pour choisir le terminal en ce cas, il suffit d'utiliser la commande set terminal, suivie par le terminal que l'on souhaite utiliser :
gnuplot> set terminal aqua Terminal type set to 'aqua' Options are '0 title "Figure 0" size 846 594 font "Times-Roman,14" noenhanced solid' gnuplot>
Comme il peut être ennuyant de spécifier le terminal à chaque démarrage de Gnuplot, on peut définir une variable de système, GNUTERM, avec le terminal à utiliser. Voici un extrait du fichier .bash_profile, qui décrit la configuration à utiliser pour le terminal Gnuplot.
export GNUTERM=aqua
Le logiciel ira donc utiliser le terminal "aqua" ; au moment de dessiner un graphique, une fenêtre de 846 pixel fois 594 pixel sera ouverte à l'écran. La police est Times-Roman en corps 14. Tout ceci est bien sûr modifiable.
Comment tracer une fonction
Et maintenant, on va voir comment il faut faire pour tracer une fonction simple, par exemple y=sin(x). Nous allons utiliser la commande plot:
gnuplot> plot sin(x) gnuplot>
Si tout s'est bien passé, nous devrions nous trouver devant la fenêtre qui est montrée ici :
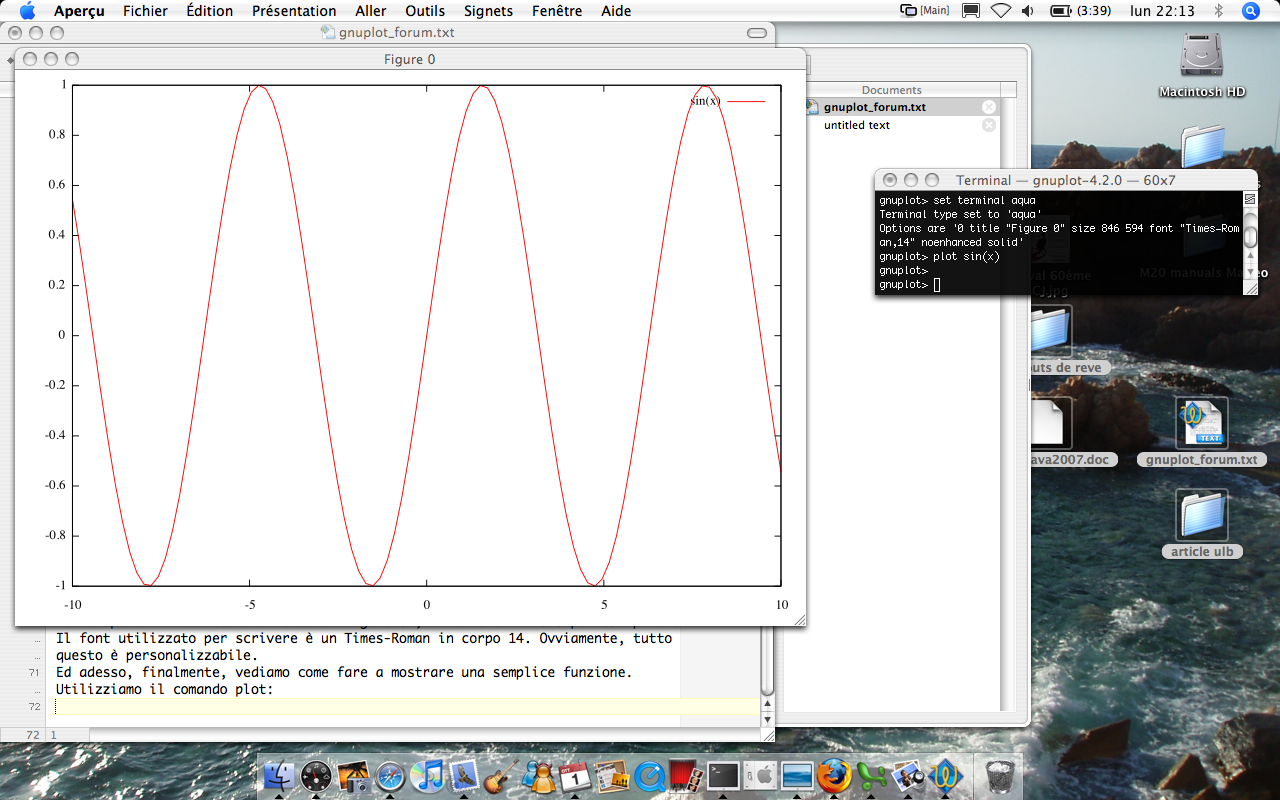
Néanmoins, le graphique que l'on vient d'obtenir n'est pas très satisfaisant pour plusieurs raisons. D'abord, il pourrait être pratique que la légende n'apparaisse pas, car il y a seulement une courbe qui est montrée. Nous allons aussi donner un titre au dessin et des noms aux axes :
gnuplot> set title "Grafico della funzione sin(x)" gnuplot> set xlabel "angolo x in radianti" gnuplot> set ylabel "sin(x)" gnuplot> unset key gnuplot> replot gnuplot>
Avec la commande set nous pouvons modifier la configuration de Gnuplot pour la session courante. La première, deuxième et troisième ligne du code que l'on vient d'écrire nous spécifient le titre du graphique et les noms des axes. La quatrième ligne (unset key) spécifie de ne pas tracer la légende, qui dans la terminologie de Gnuplot est appelée "key". La commande replot ré-dessine le graphique avec la nouvelle configuration.
Il y a un détail important qu'un oeil averti n'aura pas manqué de remarquer. Dans un graphique qui doit apparaître dans un rapport en français, il faudrait utiliser la virgule comme séparateur décimal. Cela peut être obtenu à l'aide de la commande set decimalsign, suivie du symbole à utiliser, dans notre cas donc la virgule, mis entre guillemets, car il s'agit d'une chaîne de caractères.
gnuplot> set decimalsign ',' gnuplot> replot gnuplot>
Il serait sympa aussi de visualiser la courbe entre -2*pi et 2*pi, en utilisant comme graduation de l'axe des abscisses des sous-multiples de pi. On peut obtenir tout ceci avec un code à vrai dire un peu tordu :
gnuplot> set xrange [-2*pi: 2*pi]
gnuplot> set xtics ("-2*pi" -2*pi, "-3*pi/2" -(3*pi/2), "-pi" -pi, "-pi/2" \
-pi/2, "0" 0)
gnuplot> set xtics add ("2*pi" 2*pi, "3*pi/2" (3*pi)/2, "pi" pi, "pi/2" pi/2)
gnuplot> replot
gnuplot>
La commande set xrange, suivie d'un intervalle de valeurs comprises entre crochets spécifie au logiciel de représenter seulement la portion des abscisses comprise entre les deux valeurs spécifiées. La commande set xtics introduit des gradations dans des endroits très précis de l'axe x et les représente dans le graphique avec les étiquettes que l'on voit dans la figure. On peut remarquer en passant comme set tics add nous permet d'ajouter de nouvelles étiquettes, sans retirer celles ajoutées précédemment.
La fonction sin(x) que nous avons utilisée est représentée par le logiciel en faisant un échantillonnage à intervalles régulières. Par défaut, le logiciel divise en 100 points la région montrée dans le graphique. Voici comment on peut les mettre plus en évidence :
gnuplot> plot sin(x) with points
Le nombre de points qui sont calculés peut être modifié à l'aide de la commande set samples :
gnuplot> set samples 1000 gnuplot> plot sin(x) with points gnuplot> set samples 20 gnuplot> replot gnuplot>
Maintenant, nous revenons à la visualisation avec une ligne continue, mais nous allons changer le style du trait. Le résultat dépend de la configuration du terminal que l'on va utiliser. Dans mon cas, avec Aquaterm, j'obtiens une ligne verte plutôt marquée pour l'exemple suivant :
gnuplot> plot sin(x) with lines lt 2 lw 3
Le modificateur lt est une abréviation qui indique "line type" et indique le style (souvent la couleur) de la ligne. Dans certains terminaux, surtout si l'on ne peut pas disposer de la couleur, ce qui change est un pointillage de différents types. Cette technique est fondamentale à l'impression, lorsque l'on veut produire une dissertation qui sort bien à l'impression en noir et blanc. Le modificateur lw indique plutôt "line width", c'est-à-dire la largeur de la ligne. Dans des commandes complexes comme plot, il vaut mieux de respecter attentivement l'ordre des paramètres, afin d'éviter des ambiguïtés :
gnuplot> plot sin(x) w l lt 2 lw 3
Pour terminer cette discussion, nous allons tracer le graphique de la tangente, du sinus et du cosinus aux alentours de l'origine. Comme Gnuplot tente d'ajuster automatiquement les axes, il risquerait de donner une indication faussée, car la tangente présente une asymptote verticale que le logiciel ne sait pas traiter. Il faut donc spécifier un intervalle de visualisation sur l'ordonnée :
gnuplot> set yrange [-5:5]
gnuplot> set samples 1000
gnuplot> set xrange [-2*pi: 2*pi]
gnuplot> set xtics ("-2*pi" -2*pi, "-3*pi/2" -(3*pi/2), "-pi" -pi, "-pi/2" \
-pi/2, "0" 0)
gnuplot> set xtics add ("2*pi" 2*pi, "3*pi/2" (3*pi)/2, "pi" pi, "pi/2" pi/2)
gnuplot> plot tan(x) with lines title 'tangente', sin(x) title 'seno', cos(x) \
title 'coseno'
gnuplot>
Graphiques à partir d'un fichier
Nous allons continuer cette visite guidée de Gnuplot en parlant un petit peu de graphiques tracés à partir de données expérimentales. Gnuplot est bien adapté à accomplir cette tâche et il est capable d'effectuer toute une série de traitements qui peuvent être très utiles dans beaucoup de situations.
Dans beaucoup de situations pratiques, on doit traiter des fichiers qui sont composés par beaucoup de données organisées en colonnes (par exemple), issues d'un instrument de mesure automatique ou quasi-automatique. Très souvent, il n'est pas pratique de traiter ce type de données à l'aide d'une feuille de calcul, car par exemple il y a trop de points à traiter. Nous allons voir comme Gnuplot est parfaitement à son aise dans ces situations.
Nous allons donc préparer le fichier comme il suit et nous allons l'appeler data_gnuplot.txt, dans le répertoire courant.
# Ce fichier represente l'évolution de plusieurs paramètres
#
# Temps Temperature en K Tension in mV Courant in uA
1 273 180 0.023
2 201 181 0.040
3 165 179 0.113
4 103 180 0.515
5 83 179 1.234
6 78 179 2.832
7 53 178 7.651
8 31 179 13.325
9 23 179 24.321
10 11 180 100.231
11 7 179 408.211
12 6 180 812.788
13 5 179 1211.89
14 4 178 1907.56
A ce point, nous pouvons lancer Gnuplot et obtenir un premier tracé des données présentes dans le fichier.
[davidebucci@davide-bucci-portable]$ gnuplot
G N U P L O T
Version 4.2 patchlevel 0
last modified March 2007
System: Darwin 8.10.1
Copyright (C) 1986 - 1993, 1998, 2004, 2007
Thomas Williams, Colin Kelley and many others
Type `help` to access the on-line reference manual.
The gnuplot FAQ is available from
http://www.gnuplot.info/faq/
Send comments and help requests to <gnuplot-info@lists.sourceforge.net>
Send bug reports and suggestions to <gnuplot-bugs@lists.sourceforge.net>
Terminal type set to 'aqua'
gnuplot> pwd
/Users/davidebucci/Desktop
gnuplot> cd 'Gnuplot forum/'
gnuplot> !ls
data_gnuplot.txt fenetre_data1.tiff gnuplot_forum.txt gnuplot_forum_2.txt
!
gnuplot> gnuplot> plot 'data_gnuplot.txt'
gnuplot>
Si tout s'est bien passé, vous devrez avoir obtenu un graphique similaire à ce qui suit :
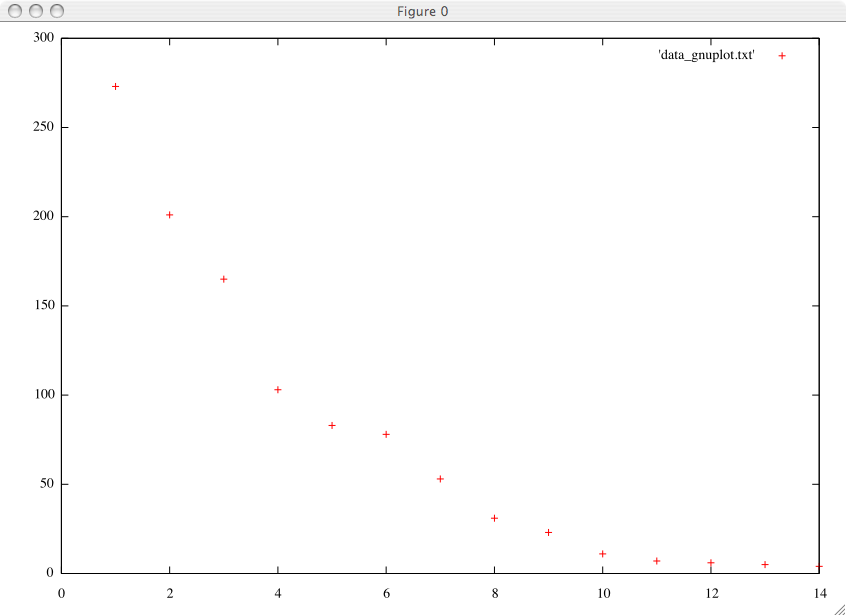
Gnuplot considère que les données sont organisées par colonnes et considère les lignes qui commencent par # comme des commentaires. Par défaut, il prend la première et deuxième colonne comme abscisse et ordonnée des données à tracer. Pour tracer les autres colonnes, il faut utiliser le modificateur using. Nous pouvons supposer de vouloir tracer la dépendance du courant (colonne 2), par rapport à la température absolue (colonne 2). Nous allons aussi placer des étiquettes sur les axes, pour obtenir quelque chose de lisible :
gnuplot> set xlabel 'Température en K' gnuplot> set ylabel 'Courant en uA' gnuplot> replot gnuplot> plot 'data_gnuplot.txt' using ($2):($4) notitle gnuplot>
Le modificateur notitle indique de ne pas tracer de légende pour cette courbe. Nous pouvons unir les points, en laissant indiqués les données expérimentales :
gnuplot> plot 'data_gnuplot.txt' using ($2):($4) notitle with lines, \ 'data_gnuplot.txt' using ($2):($4) notitle with points gnuplot> set xrange [0:50] gnuplot> replot gnuplot>
Cette dernière commande plot lit le fichier deux fois. Pendant la première, il trace les lignes entre les points, tandis qu'au cours de la deuxième il identifie et trace les points expérimentaux. J'en ai profité pour effectuer un agrandissement sur la partie de courbe que nous allons supposer être la plus intéressante.
Il est sous entendu que chaque mesure est affecté par une erreur. Imaginons d'avoir discuté longuement avec les techniciens qui ont effectué les mesures et avoir conclu que l'incertitude sur la mesure de température est de 3%, tandis que pour le courant est de 5%. Gnuplot permet de tracer des graphiques avec des barres d'incertitudes. Normalement, il s'attend de trouver l'erreur absolue indiquée dans une colonne du fichier :
(x, y, xdelta, ydelta)
mais nous pouvons éviter de modifier les fichiers, en utilisant à nouveau le modificateur using. Nous allons donc calculer à la volée les erreurs absolues à partir des erreurs relatives et les données que nous pouvons lire dans le fichier :
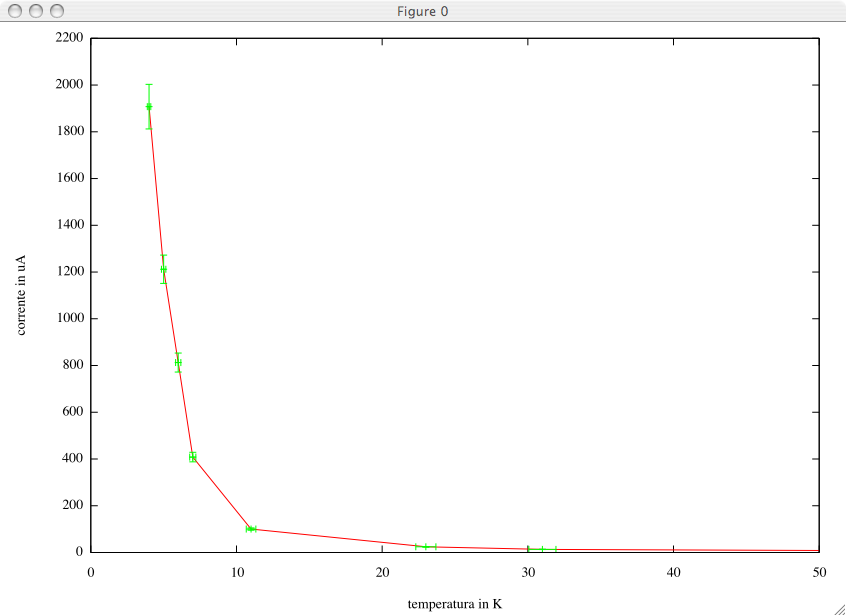
gnuplot> temperror=0.03 gnuplot> currerror=0.05 gnuplot> plot 'data_gnuplot.txt' using ($2):($4) notitle with lines, \ 'data_gnuplot.txt' using ($2):($4):(temperror*$2):(currerror*$4) notitle \ with xyerrorbars gnuplot>
car xdelta et ydelta sont obtenues à partir de l'erreur relatif fois la donnée présente dans la colonne appropriée. Voici le résultat de nos efforts :
Example de lissage sur des données expérimentales
Normalement, connecter entre eux les points d'une mesure est surtout utile pour fournir une guide pour l'oeil. Souvent il peut être plus intéressant d'effectuer un lissage à partir d'une courbe fournie par exemple par la théorie. Ceci permet entre autre d'obtenir des données qui peuvent être utiles à des vérifications théoriques ou à des prédictions. Nous pouvons par exemple supposer que la dépendance du courant dans notre expérience inventée suit une loi de type 1mA*exp(-b*(x-c))+d, où b, c et d sont des paramètres plus ou moins libres. Nous allons demander à Gnuplot de réaliser un lissage numérique en se basant sur les données dont nous disposons. Il va s'occuper d'appliquer un algorithme de minimisation avec un critère de moindres carrés, pour calculer les valeurs des paramètres qui permettent d'adapter au mieux la courbe théorique sur les points expérimentaux.
gnuplot> f(x)=exp(-b*(x-c))+d
gnuplot> b=1
gnuplot> c=10
gnuplot> d=0.023
gnuplot> fit f(x) 'data_gnuplot.txt' using ($2):($4) via b,c,d
Iteration 0
WSSR : 4.12945e+06 delta(WSSR)/WSSR : 0
delta(WSSR) : 0 limit for stopping : 1e-05
lambda : 564.399
initial set of free parameter values
b = 1
c = 10
d = 0.023
*/
Iteration 1
WSSR : 2.66856e+06 delta(WSSR)/WSSR : -0.547443
delta(WSSR) : -1.46089e+06 limit for stopping : 1e-05
lambda : 564.399
resultant parameter values
b = 1.12016
c = 10.0214
d = 0.0231075
******** Je coupe pour que ceci ne prenne pas trop de place **********
Iteration 86
WSSR : 8506.14 delta(WSSR)/WSSR : -4.18425e-08
delta(WSSR) : -0.000355918 limit for stopping : 1e-05
lambda : 0.000564399
resultant parameter values
b = 0.471138
c = 20.0252
d = 16.6859
After 86 iterations the fit converged.
final sum of squares of residuals : 8506.14
rel. change during last iteration : -4.18425e-08
degrees of freedom (FIT_NDF) : 4
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 46.1144
variance of residuals (reduced chisquare) = WSSR/ndf : 2126.54
Final set of parameters Asymptotic Standard Error
======================= ==========================
b = 0.471138 +/- 0.02751 (5.838%)
c = 20.0252 +/- 0.9298 (4.643%)
d = 16.6859 +/- 28.82 (172.7%)
correlation matrix of the fit parameters:
b c d
b 1.000
c -0.998 1.000
d 0.557 -0.590 1.000
gnuplot> plot f(x) title 'Modèle théorique', 'data_gnuplot.txt' using \
($2):($4):(temperror*$2):(currerror*$4) title 'Données expérimentales' with \
xyerrorbars
gnuplot>
Le résultat est celui d'une courbe qui donne une approximation plutôt bonne de l'allure des résultats de mesure :
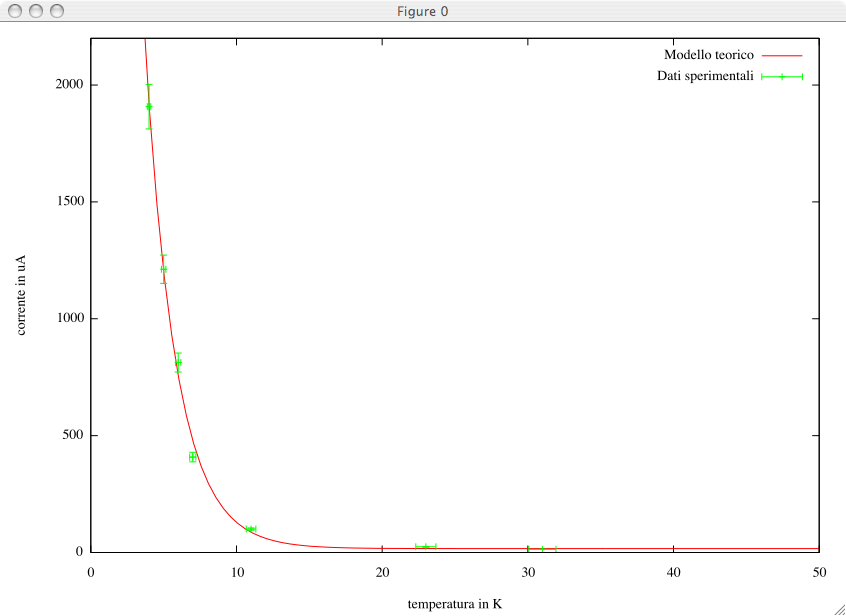
Nous avons défini une fonction f(x) qui dépend des trois paramètres b, c et d. Nous avons ensuite utilisé la commande fit pour effectuer le lissage. Un détail très important de cette opération est de choisir de façon correcte les valeurs initiales des paramètres à optimiser : la minimisation de l'erreur peut très vite tomber et se bloquer sur des minima locaux qui ne sont pas la solution que l'on cherche. Il peut être judicieux d'effectuer des tests sur différentes conditions initiales pour voir si l'on converge toujours sur les mêmes valeurs des paramètres libres. Pour la même raison, la commande fit permet de spécifier les paramètres à faire varier pendant l'optimisation (à travers via). Dans beaucoup de cas pratiques, il ne faut pas être trop gourmands et faire varier seulement un paramètre à la fois, pour ensuite peaufiner les résultats trouvés tous ensemble.
Un dernier point. La simplicité d'utilisation de la commande fit ne doit pas faire perdre de vue le fait qu'un lissage numérique demande un peu d'expérience, pour éviter de faire des grosses erreurs. Jeter un coup d'oeil à l'indication de l'erreur asymptotique permet de se rendre compte de la fiabilité des résultats, mais... avec un bon nombre de paramètres libres on peut "fitter" un éléphant !
J'oubliais : il peut être utile d'utiliser la commande print pour faire quelques calculs, ou pour montrer la valeur d'un paramètre.
gnuplot> print b 0.471138066465779 gnuplot> print f(53) 16.6859006122384 gnuplot> print sqrt(500) 22.3606797749979
Dans le prochain paragraphe, nous allons parler des techniques nécessaires pour obtenir des fichier Postscript, à utiliser par exemple à l'intérieur d'un document LaTeX.
Exporter un graphique en Postscript
Les premières fois que l'on utilise Gnuplot, beaucoup de personnes s'étonnent que le logiciel apparemment ne prévoit pas une fonction pour imprimer les graphiques obtenus. En réalité, Gnuplot utilise un mécanisme très flexible qui repose sur le concept de terminal. Parmi les terminaux disponibles, il y en a qui peuvent fournir des fichiers directement imprimables, par exemple en format Postscript. Dans notre discussion, nous allons traiter le format EPS (Encapsulated Postscript), qui est un format vectoriel et qui s'intègre très bien avec LaTeX par exemple. Le format EPS est aussi adapté à être envoyé directement à une imprimante laser qui dispose d'un interprète de ce format, pour obtenir une impression de qualité irréprochable. Le logiciel Aperçu, sous MacOSX, permet d'ouvrir sans difficultés les fichiers EPS. Dans d'autres systèmes d'exploitations, des logiciels gratuits comme Ghostscript peuvent être précieux dans la manipulation de fichiers PS et EPS.
Comme nous devons écrire un peu de commandes l'une après l'autre, il est opportun d'utiliser la possibilité qui a Gnuplot d'utiliser des scripts. Nous allons nous référer à l'exemple de lissage numérique, présenté précédemment, mais cette fois la sortie sera faite sur fichier EPS. Nous allons donc créer le fichier fit_temperature.gp. Pour ce qui me concerne, j'utilise l'extension .txt pour les fichiers qui contiennent les données et .gp pour les scripts de Gnuplot, mais vous êtes libres de faire le choix que vous préférez.
# Dans ce script, nous allons faire un lissage numérique sur des données,
# nous allons montrer le résultat sur le vidéo et nous allons préparer un
# fichier EPS, prêt pour l'impression qui contient le graphique.
f(x)=exp(-b*(x-c))+d
b=1
c=10
d=0.023
fit f(x) 'data_gnuplot.txt' using ($2):($4) via b,c,d
temperror=0.03
currerror=0.05
set xrange [0:50]
set yrange [0:2200]
set xlabel 'Temperatura in K'
set ylabel 'Corrente in {/Symbol m}A'
plot f(x) title 'Modèle théorique', 'data_gnuplot.txt' using \
($2):($4):(temperror*$2):(currerror*$4) title 'Données expérimentales' with \
xyerrorbars
# Nous sauvons le terminal dans une pile
set terminal push
# Nous allons utiliser un terminal Postscript
set terminal postscript portrait enhanced mono "Helvetica" 15
# Nous réduisons les dimensions du dessin par rapport aux dimensions d'une page
# UNI A4
set size 1.0, 0.4
# Nous spécifions le nom du fichier qui contiendra le graphique
set output "fit_temperature.eps";
# Redessin
replot;
set output
# Nous récupérons le terminal utilisé précédemment
set terminal pop
# Nous utilisons les dimensions normales
set size 1,1
Les commentaires que j'ai écrits devraient permettre de suivre plus ou moins la fonction de chaque ligne du script. Pour lancer l'exécution du script (qui doit être dans un répertoire du chemin courant, où le fichier data_gnuplot.txt est aussi présent, on peut utiliser la commande load :
gnuplot> load 'fit_temperature.gp'
Gnuplot va charger les données, il fera le lissage, il montrera le résultat à l'écran, pour ensuite le sauvegarder sur le disque dans le fichier fit_temperature.eps.
Quelqu'un avec un oeil avisé aura remarqué que dans les graphiques présentés précédemment j'avais utilisé le symbole uA pour représenter les microamper. J'avais donc utilisé la lettre u à la place de µ (mu en Grec), ce qui n'est pas acceptable dans une impression de qualité. J'ai donc adopté une petite astuce qui consiste à utiliser dans la légende de l'axe y le code Postscript correspondant à la lettre mu. A l'écran, le résultat n'est pas correcte, mais ce qui nous intéresse le plus est ce qui donnera le fichier Postscript, qui est parfait. Voici le résultat, en format EPS ainsi que dans une version convertie en PNG. Il est clair que sur le fichier EPS original on peut agrandir tant que l'on désire sans que les détails ne perdent pas de définition, car il s'agit d'un fichier vectoriel, dont la dimension est de 20 KiB. Si nous faisons une comparaison de cette valeur avec les 48 KiB du fichier PNG, qui n'est même pas è une résolution très élevée, nous voyons l'intérêt d'utiliser des formats vectoriels quand possible.
Une autre technique intéressante consiste à utiliser la pile mise à disposition par Gnuplot pour sauvegarder l'état d'un terminal, pour ensuite le récupérer facilement (sous une version récente de Gnuplot). Ceci est très intéressant pour nous, car il nous permet de basculer de façon temporaire sur un terminal Postscript et ensuite revenir rapidement à la situation de départ.
Pendant la configuration du terminal, à la ligne :
set terminal postscript portrait enhanced mono "Helvetica" 15
nous avons utilisé plusieurs options du terminal Postscript. En particulier, nous avons spécifié d'utiliser une version améliorée du terminal, qui permet d'utiliser des traits particuliers pour les courbes. Nous avons choisi (avec le modificateur mono) d'obtenir une représentation monochromatique du graphique. Personnellement, j'apporte un grand soin à faire en sorte que mes graphiques ne nécessitent pas de la couleur pour être compréhensibles. Ceci simplifie les choses en impression, en photocopie etc... Ehnanced veut dire que le terminal reconnaît des commandes Postscript, pour obtenir des effets particuliers. Il est très utile à mon avis l'accent circonflexe ^, pour obtenir des exposants utiles dans certaines unités de mesure.
Helvetica 15 indique d'utiliser la bien connue police sans graces Helvetica en corps 15.
Représentation avancée de surfaces
Dans ce paragraphe, nous allons décrire des exemples un peu plus avancés, pour représenter par exemple des surfaces. Nous allons commencer avec une fonction qui est un grand classique pour ce genre d'exemples (je l'ai tracée pour la première fois sur un VIC-20...) :
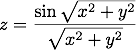
gnuplot> splot sin(sqrt(x*x+y*y))/sqrt(x*x+y*y)
Le résultat est plutôt essentiel :
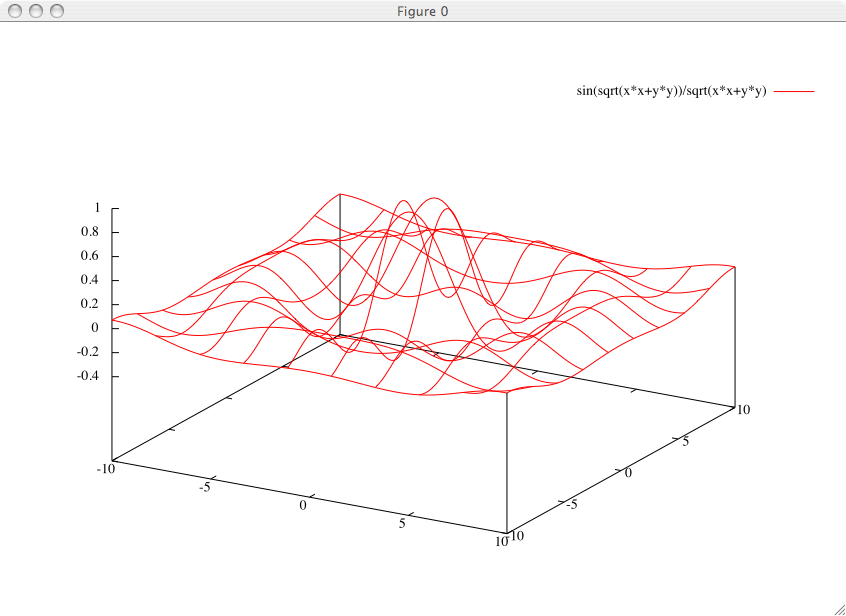
Par défaut, Gnuplot trace des surfaces en représentation "fil de fer". Nous pouvons augmenter la résolution avec laquelle la fonction est tracée, c'est-à-dire le nombre de fils utilisés, à travers la commande set samples e set isosamples :
gnuplot> set samples 50 gnuplot> set isosamples 50 gnuplot> splot sin(sqrt(x*x+y*y))/sqrt(x*x+y*y) gnuplot>
Une chose qui peut améliorer considérablement la qualité du résultat tracé est l'élimination des lignes cachées. De cette façon, la fonction est représentée avec une surface, bien que le temps nécessaire pour le dessin augmente considérablement. Il est possible de changer l'angle d'observation de la fonction représentée en 3D, à travers la commande set view, ainsi que le montrer avec show view :
gnuplot> show view
view is 60 rot_x, 30 rot_z, 1 scale, 1 scale_z
gnuplot> set view 80, 20,1,1
gnuplot> replot
gnuplot>
Cette vue montre que l'algorithme d'élimination des lignes cachées effectue une distinction entre le "dessus" et le "dessous" de la surface, qui sont tracés dans des couleurs différentes :
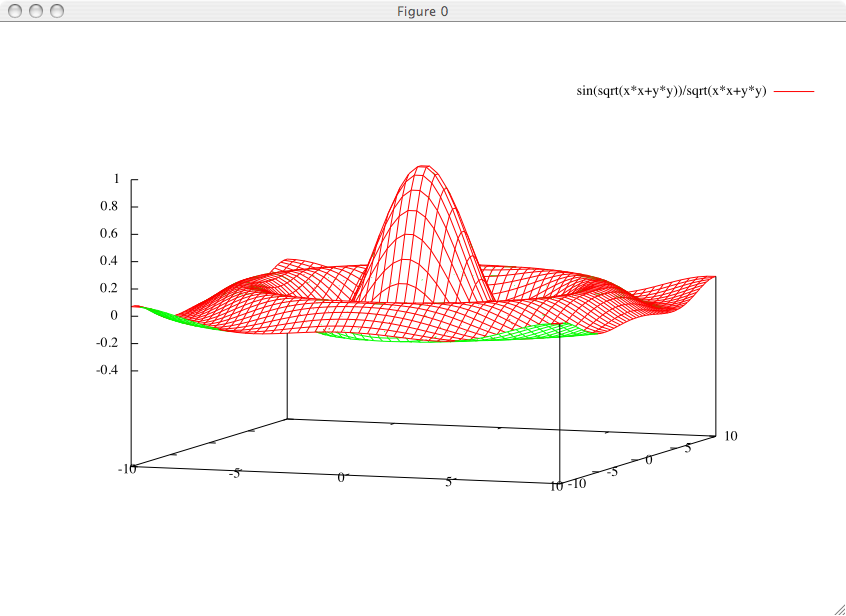
Gnuplot permet de représenter les isocontours en plus que la surface, ce qui permet de simplifier grandement la représentation en beaucoup de cas pratiques :
gnuplot> set contour gnuplot> set cntrparam levels discrete 0, 0.125, 0.25, 0.5,0.75, -0.125 gnuplot> replot gnuplot> set contour both gnuplot> replot gnuplot> unset surface gnuplot> replot gnuplot>
Dans l'exemple que l'on vient de traiter, nous pouvons voir que Gnuplot peut représenter des isocontours sous la surface ou sur la surface. Cette dernière peut aussi ne pas être tracés (avec set/unset surface, tandis que les isocontours sont activés/désactivés avec set/unset contour).
J'ai aussi utilisé set cntrparam pour spécifier explicitement quels niveaux je veux que le logiciel trace. Les possibilités sont nombreuses, je ne vais pas les traiter toutes en détail et je vous conseille de vous référer à l'aide du logiciel, qui est complet, relativement compréhensible, ainsi que fourni d'exemples intéressants :
gnuplot> help set cntrparam
`set cntrparam` controls the generation of contours and their smoothness for
a contour plot. `show contour` displays current settings of `cntrparam` as
well as `contour`.
Syntax:
set cntrparam { { linear
| cubicspline
| bspline
| points <n>
| order <n>
| levels { auto { <n>} | <n>
| discrete <z1> {, <z2>{, <z3>...}}
| incremental <start>, <incr> {, <end>}
}
}
}
show contour
This command has two functions. First, it sets the values of z for which
contour points are to be determined (by linear interpolation between data
points or function isosamples.) Second, it controls the way contours are
drawn between the points determined to be of equal z.
********* Ici je coupe... *********
Examples:
set cntrparam bspline
set cntrparam points 7
set cntrparam order 10
To select levels automatically, 5 if the level increment criteria are met:
set cntrparam levels auto 5
To specify discrete levels at .1, .37, and .9:
set cntrparam levels discrete .1,1/exp(1),.9
To specify levels from 0 to 4 with increment 1:
set cntrparam levels incremental 0,1,4
To set the number of levels to 10 (changing an incremental end or possibly
the number of auto levels):
set cntrparam levels 10
To set the start and increment while retaining the number of levels:
set cntrparam levels incremental 100,50
See also `set contour` for control of where the contours are drawn, and
`set clabel` for control of the format of the contour labels and linetypes.
Press return for more:
See also
contours demo (contours.dem)
and
contours with user defined levels demo (discrete.dem).
gnuplot>
Si l'on veut représenter seulement les isocontours, il peut être plus flexible de faire en sorte que Gnuplot les obtienne, stocker les résultats dans un fichier à traiter dans un deuxième moment avec la commande plot . Je reprends ici un exemple depuis l'aideen ligne du logiciel. Je l'ai complété un peu et nous pouvons le mémoriser dans un script appelé niveaux.gp :
# Ce script visualise une fonction z=f(x,y) en utilisant des isocontours. # Un fichier tampon appelé niveaux.txt est utilisé unset surface set contour set samples 100 set isosamples 100 set cntrparam levels discrete 0, 0.125, 0.25, 0.5,0.75, -0.125 set table 'livelli.txt' splot sin(sqrt(x*x+y*y))/sqrt(x*x+y*y) unset table # Les informations sur les isocontours sont maintenant dans niveaux.txt plot 'niveaux.txt' with lines notitle
Le script génère le fichier tampon niveaux.txt, qui contient les données relatives aux isocontours que nous voulons tracer. Les courbes sont tracées seulement dans un deuxième moment, avec la commande plot, en exploitant les données mémorisées dans le fichier.
Pour terminer, à partir de la version 4.0 de Gnuplot, il est possible de représenter des surfaces de façon très attirante, surtout sur un écran couleurs, ou dans une impression de bonne qualité. Il s'agit de colorer la surface (ou pour être plus précis, chaque polygone qui la compose) avec une couleur qui dépende de la valeur de la fonction en chaque point. Pour activer cette modalité, il faut utiliser la commande set pm3d:
gnuplot> unset contour gnuplot> set pm3d gnuplot> set surface gnuplot> set view 60,60,1,1 gnuplot> splot sin(sqrt(x*x+y*y))/sqrt(x*x+y*y) notitle gnuplot>
Dont le résultat est le suivant :
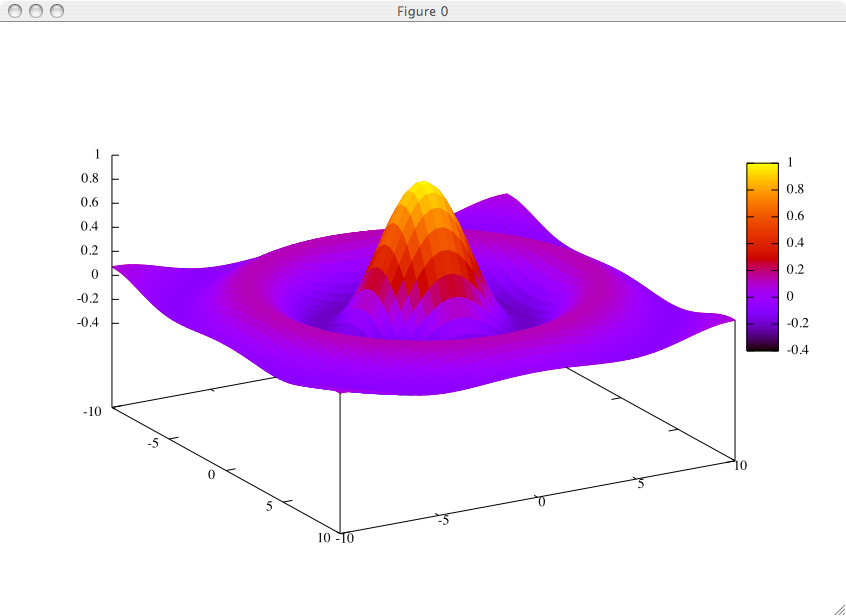
Conclusion
Gnuplot est un logiciel très puissant, capable de produire des graphiques extrêmement complexes et de très bonne qualité. Néanmoins, il s'agit d'un logiciel qui demande un certain période d'apprentissage pour en apprendre et apprécier la philosophie. J'espère avoir fourni ici une contribution avec mes pages.
License:
--------
Copyright (C) 2007 Davide Bucci davbucci at tiscali dot it
This program is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program; if not, write to the Free Software
Foundation, Inc., 675 Mass Ave, Cambridge, MA 02139, USA.
