Un'introduzione a Gnuplot
Un programma OpenSource per tracciare grafici
Qualche concetto per cominciare
Come tracciare una funzione
Grafici a partire da un file
Un esempio di fit di dati sperimentali
Esportare un grafico in Postscript
Rappresentazione avanzata di superfici
Conclusioni
Introduzione
Gnuplot è un software utile per tracciare grafici di ogni tipo e se utilizzato correttamente fornisce dei risultati di tipo assolutamente professionale, spesso nettamente superiori a quelli ottenibili per esempio con Excel. Come Maxima, si tratta di un programma che esiste ormai da parecchio tempo (dal 1986 per la precisione) ed è completamente multipiattaforma. Questo è un vantaggio non da poco... nel mio lavoro mi trovo a saltare continuamente fra Windows, Linux e MacOSX ed è da diversi anni che quando posso utilizzo (senza rimpianto) solo strumenti che non mi leghino ad un sistema operativo in particolare. Il principale ostacolo di Gnuplot è che è un programma interattivo a linea di comando che si usa da terminale ed è molto ostico da utilizzare le prime volte. Vedremo come cercare di migliorare la situazione...
Questa pagina è stata scritta assemblando diversi miei interventi sul forum di Macitynet, a cui partecipo spesso con lo pseudonimo di DarwinNE:
![]() http://www.macitynet.it/forum/showthread.php?t=59206
http://www.macitynet.it/forum/showthread.php?t=59206
Come ho fatto con Maxima, evito di descrivere in dettaglio ogni comando (per quello basta battere help, seguito dal comando desiderato). Preferisco fornire degli esempi concreti e completi, che possono essere utili per capire la filosofia che sta dietro al programma.
Qualche concetto per cominciare
La prima cosa che è importante da sapere è che Gnuplot non disegna direttamente sullo schermo o su una finestra, ma piuttosto dialoga con un *terminale* grafico. Quest'ultimo è un modulo scritto per mettere a disposizione un certo numero di funzioni grafiche che poi Gnuplot utilizzerà. Per questo motivo, quando viene lanciato, il programma fornisce qualche informazione sulla versione e specifica quale terminale è attualmente in uso:
[davidebucci@davide-bucci-portable]$ gnuplot
G N U P L O T
Version 4.2 patchlevel 0
last modified March 2007
System: Darwin 8.10.1
Copyright (C) 1986 - 1993, 1998, 2004, 2007
Thomas Williams, Colin Kelley and many others
Type `help` to access the on-line reference manual.
The gnuplot FAQ is available from
http://www.gnuplot.info/faq/
Send comments and help requests to <gnuplot-info@lists.sourceforge.net>
Send bug reports and suggestions to <gnuplot-bugs@lists.sourceforge.net>
Terminal type set to 'aqua'
gnuplot>
Per uscire dal programma, basta introdurre il comando quit:
gnuplot> quit [davidebucci@davide-bucci-portable]$
La mia versione di Gnuplot è la 4.2 (abbastanza recente, nel momento in cui scrivo) ed il terminale è Aquaterm, un terminale grafico che funziona molto bene con MacOSX e che va scaricato, per esempio da VersionTracker, ed installato a parte. Per usare Gnuplot con Linux, spesso il terminale utilizzato è x11, ovvero XWindows, ma sotto MacOSX non è necessario perché Aquaterm funziona molto bene ed è pił leggero.
Per ottenere una lista dei terminali disponibili, tanto per curiosità, basta scrivere set terminal seguito da invio. Attenzione che Gnuplot è case sensitive, ovvero fa distinzioni fra le minuscole e le maiuscole.
gnuplot> set terminal
Available terminal types:
aqua Interface to graphics terminal server for Mac OS X
dumb ascii art for anything that prints text
emf Enhanced Metafile format
emtex LaTeX picture environment with emTeX specials
epslatex LaTeX picture environment using graphicx package
fig FIG graphics language for XFIG graphics editor
gif GIF images using libgd and TrueType fonts
jpeg JPEG images using libgd and TrueType fonts
latex LaTeX picture environment
mf Metafont plotting standard
png PNG images using libgd and TrueType fonts
postscript PostScript graphics, including EPSF embedded files (*.eps)
svg W3C Scalable Vector Graphics driver
x11 X11 Window System
gnuplot>
Nell'esempio sopra, in realtà la lista è molto pił lunga, ma l'ho ridotta un po', limitandomi ai terminali pił interessanti. Vedremo qualche esempio in seguito. Può accadere che con alcune installazioni incomplete, Gnuplot parta con un terminale non definito. In questo caso, all'avvio, dopo le informazioni sulla versione si avrà qualcosa del tipo:
Terminal type set to 'unknown' gnuplot>
Per scegliere il terminale da utilizzare in questo caso, basta usare il comando set terminal, seguito dal terminale richiesto:
gnuplot> set terminal aqua Terminal type set to 'aqua' Options are '0 title "Figure 0" size 846 594 font "Times-Roman,14" noenhanced solid' gnuplot>
Dato che può essere noioso specificare sempre il terminale ad ogni esecuzione di Gnuplot, si può definire una variabile di sistema, GNUTERM con il terminale da utilizzare. Ecco un estratto del mio file .bash_profile, che configura per l'appunto il terminale di default ad aquaterm.
export GNUTERM=aqua
Il programma è configurato a questo punto per utilizzare il terminale aqua; verrà aperta una finestra di titolo "Figure 0", di dimensioni 846 per 594 pixel. Il font utilizzato per scrivere è un Times-Roman in corpo 14. Ovviamente, tutto questo è personalizzabile.
Come tracciare una funzione
Ed adesso, finalmente, vediamo come fare a mostrare una semplice funzione, per esempio y=sin(x). Utilizzeremo il comando plot:
gnuplot> plot sin(x) gnuplot>
Se tutto è andato bene, dovremmo trovarci di fronte ad una finestra come quella mostrata qui sotto:
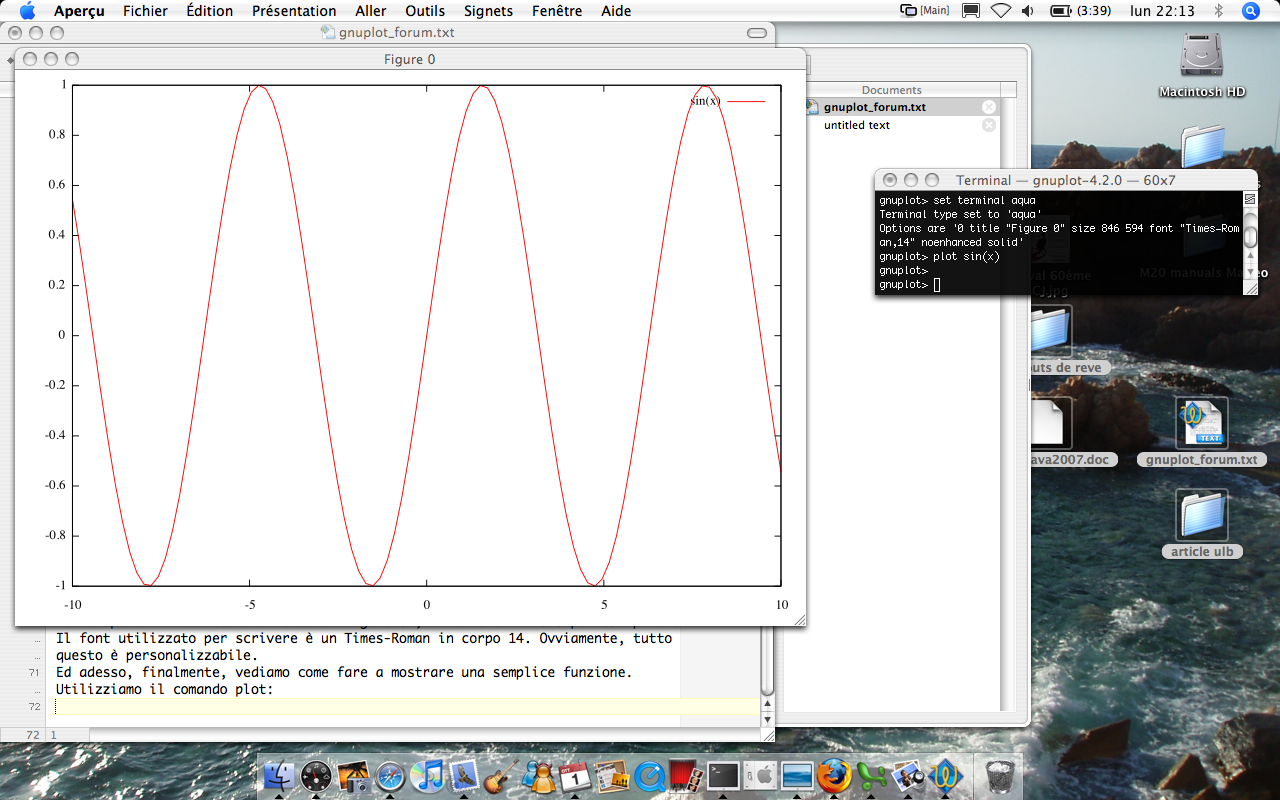
Tuttavia, il grafico ottenuto non è molto soddisfacente per alcune ragioni. In primo luogo, potrebbe essere comodo fare in modo che la legenda non compaia, dato che c'è solo una curva mostrata. Mettiamo inoltre un titolo e diamo dei nomi agli assi:
gnuplot> set title "Grafico della funzione sin(x)" gnuplot> set xlabel "angolo x in radianti" gnuplot> set ylabel "sin(x)" gnuplot> unset key gnuplot> replot gnuplot>
Con il comando set modifichiamo la configurazione temporanea che Gnuplot utilizza per tracciare un grafico. La prima, seconda e terza riga specificano il titolo e gli assi, la quarta riga (unset key) specifica di non tracciare la legenda (che Gnuplot chiama "key") mentre il comando replot ridisegna il grafico corrente con le nuove impostazioni.
C'è ancora una cosa che non sfugge all'occhio allenato. In un grafico che debba comparire in un rapporto in italiano, sarebbe meglio utilizzare la virgola come separatore decimale. Si rimedia con il comando set decimalsign, seguito dal simbolo da utilizzare, nel nostro caso la virgola messa tra apici, perché si tratta di una stringa.
gnuplot> set decimalsign ',' gnuplot> replot gnuplot>
Sarebbe anche carino visualizzare la curva fra -2*pi e 2*pi, utilizzando come gradazione dell'ascissa i dei sottomultipli di pi. Si riesce a fare tutto con un po' di funambolismo:
gnuplot> set xrange [-2*pi: 2*pi]
gnuplot> set xtics ("-2*pi" -2*pi, "-3*pi/2" -(3*pi/2), "-pi" -pi, "-pi/2" \
-pi/2, "0" 0)
gnuplot> set xtics add ("2*pi" 2*pi, "3*pi/2" (3*pi)/2, "pi" pi, "pi/2" pi/2)
gnuplot> replot
gnuplot>
Il comando set xrange seguito da un intervallo di valori fra parentesi quadre indica di rappresentare soltanto la porzione indicata del grafico. Il comando set xtics introduce delle gradazioni in dei punti molto precisi dell'asse x e le rappresenta nel grafico con le etichette mostrate. Si noti come set tics add permette di aggiungere delle nuove gradazioni senza eliminare quelle precedentemente introdotte.
La funzione sin(x) che abbiamo introdotta è ovviamente campionata ad intervalli regolari. Di default, l'intervallo rappresentato nel grafico è suddiviso in 100 punti. Ecco come visualizzarli:
gnuplot> plot sin(x) with points
Il numero di punti calcolati può essere modificato con il comando set samples:
gnuplot> set samples 1000 gnuplot> plot sin(x) with points gnuplot> set samples 20 gnuplot> replot gnuplot>
Ritorniamo invece alla visualizzazione con linea continua, ma cambiamo lo stile della linea. Il risultato dipende un po' dalle impostazioni del terminale che si sta utilizzando. Nel mio caso, su Aquaterm ottengo una linea verde piuttosto marcata:
gnuplot> plot sin(x) with lines lt 2 lw 3
Il modificatore lt sta per "line type" ed indica il tipo (colore) della linea. Su alcuni terminali, invece di modificarne il colore si ottiene un tratteggiato di diversi tipi, utilissimi per distinguere le curve in stampa quando alle volte non si possono usare i colori. Il modificatore lw sta per "line width", ovvero larghezza della linea. In comandi complessi come plot, è bene rispettare l'ordine dei vari parametri, che possono però essere abbreviati quando non c'è rischio di ambiguità:
gnuplot> plot sin(x) w l lt 2 lw 3
Per finire, tracciamo il grafico della tangente, del seno e del coseno attorno all'origine. Dobbiamo specificare un'intervallo per l'asse delle y, perché se no il grafico è poco significativo ed è troppo affetto dall'intervallo di campionamento e dagli infiniti della tangente, che il programma non può trattare automaticamente.
gnuplot> set yrange [-5:5]
gnuplot> set samples 1000
gnuplot> set xrange [-2*pi: 2*pi]
gnuplot> set xtics ("-2*pi" -2*pi, "-3*pi/2" -(3*pi/2), "-pi" -pi, "-pi/2" \
-pi/2, "0" 0)
gnuplot> set xtics add ("2*pi" 2*pi, "3*pi/2" (3*pi)/2, "pi" pi, "pi/2" pi/2)
gnuplot> plot tan(x) with lines title 'tangente', sin(x) title 'seno', cos(x) \
title 'coseno'
gnuplot>
Grafici a partire da un file
Continuiamo questa visita guidata di Gnuplot parlando un po' dei grafici che possono essere tracciati a partire da dei dati sperimentali. Gnuplot è particolarmente adatto in questo e consente di effettuare tutta una serie di trattamenti molto interessanti su quanto mostrato a schermo.
In moltissimi casi nella pratica sperimentale, capita di ottenere dei file composti da dati organizzati in colonne, per esempio come output da strumenti di misura automatici o semiautomatici. Spesso e volentieri, risulta molto poco pratico trattare questo genere di dati con programmi di tipo foglio elettronico perché per esempio i punti sono troppi. Vediamo quindi come far entrare in gioco Gnuplot.
Prepariamo il file che segue e salviamolo con il nome data_gnuplot.txt nella directory corrente.
# Questo file rappresenta l'evoluzione di alcuni parametri inventati
#
# Tempo Temperatura in K Tensione in mV Corrente in uA
1 273 180 0.023
2 201 181 0.040
3 165 179 0.113
4 103 180 0.515
5 83 179 1.234
6 78 179 2.832
7 53 178 7.651
8 31 179 13.325
9 23 179 24.321
10 11 180 100.231
11 7 179 408.211
12 6 180 812.788
13 5 179 1211.89
14 4 178 1907.56
A questo punto, lanciamo Gnuplot e possiamo utilizzare il comando plot per tracciare i dati presenti nel file:
[davidebucci@davide-bucci-portable]$ gnuplot
G N U P L O T
Version 4.2 patchlevel 0
last modified March 2007
System: Darwin 8.10.1
Copyright (C) 1986 - 1993, 1998, 2004, 2007
Thomas Williams, Colin Kelley and many others
Type `help` to access the on-line reference manual.
The gnuplot FAQ is available from
http://www.gnuplot.info/faq/
Send comments and help requests to <gnuplot-info@lists.sourceforge.net>
Send bug reports and suggestions to <gnuplot-bugs@lists.sourceforge.net>
Terminal type set to 'aqua'
gnuplot> pwd
/Users/davidebucci/Desktop
gnuplot> cd 'Gnuplot forum/'
gnuplot> !ls
data_gnuplot.txt fenetre_data1.tiff gnuplot_forum.txt gnuplot_forum_2.txt
!
gnuplot> gnuplot> plot 'data_gnuplot.txt'
gnuplot>
Se tutto va bene, dovreste aver ottenuto un grafico pari a quello riportato qui sotto:
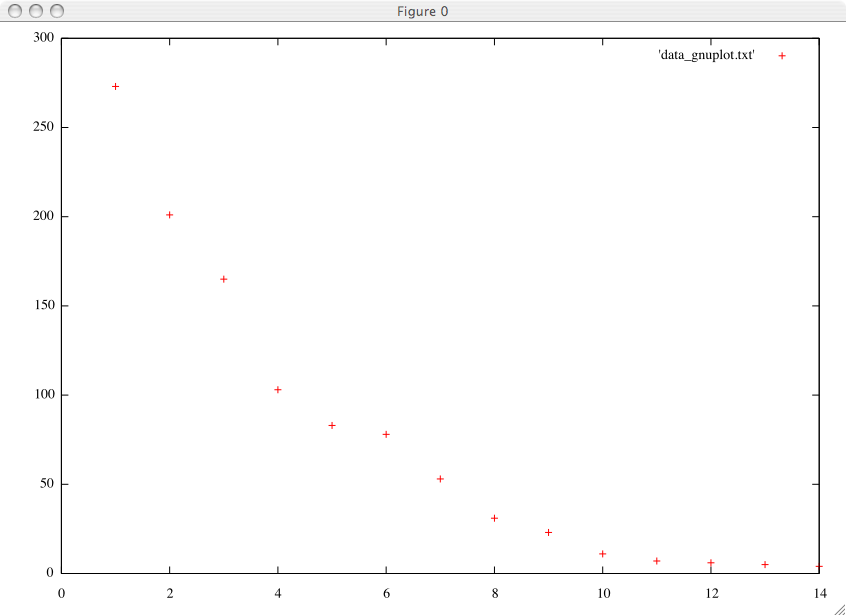
Gnuplot di default traccia i dati in colonne, considera le linee che iniziano con # come dei commenti e traccia la seconda colonna rispetto alla prima. In questo caso, si tratta dunque della temperatura rispetto al tempo. Per tracciare le altre colonne, bisogna utilizzare il modificatore using. Supponiamo di voler tracciare la dipendenza della corrente (colonna 4) rispetto alla temperatura (colonna 2). Diamo inoltre un nome agli assi, per avere qualcosa di significativo:
gnuplot> set xlabel 'temperatura in K' gnuplot> set ylabel 'corrente in uA' gnuplot> replot gnuplot> plot 'data_gnuplot.txt' using ($2):($4) notitle gnuplot>
Il modificatore notitle indica di non tracciare la legenda per questa curva. Possiamo unire i punti, lasciando indicati i dati sperimentali:
gnuplot> plot 'data_gnuplot.txt' using ($2):($4) notitle with lines, \ 'data_gnuplot.txt' using ($2):($4) notitle with points gnuplot> set xrange [0:50] gnuplot> replot gnuplot>
Quest'ultimo comando plot legge il file due volte. La prima volta traccia le linee fra i punti, mentre la seconda identifica i punti sperimentali. Ho provveduto a fare un zoom in una parte che supporremo significativa della curva sperimentale.
E' sottointeso che ogni misura è affetta da un errore. Dopo lunghe discussioni con chi si occupa della macchina, supponiamo di aver concluso che l'errore sulla temperatura è del 3% mentre sulla corrente è del 5%. Gnuplot permette di tracciare dei grafici con delle barre di errore; normalmente, l'entità dell'errore assoluto compare come una colonna del file:
(x, y, xdelta, ydelta)
ma a questo possiamo facilmente fare a meno, utilizzando il modificatore using, che ci permette di utilizzare semplicemente l'errore relativo senza dover toccare i dati sul file:
gnuplot> temperror=0.03 gnuplot> currerror=0.05 gnuplot> plot 'data_gnuplot.txt' using ($2):($4) notitle with lines, \ 'data_gnuplot.txt' using ($2):($4):(temperror*$2):(currerror*$4) notitle \ with xyerrorbars gnuplot>
Perché xdelta e ydelta in questo caso devono essere l'errore relativo che conosciamo, moltiplicato per la colonna corrispondente. Ecco qui il risultato dei nostri sforzi:
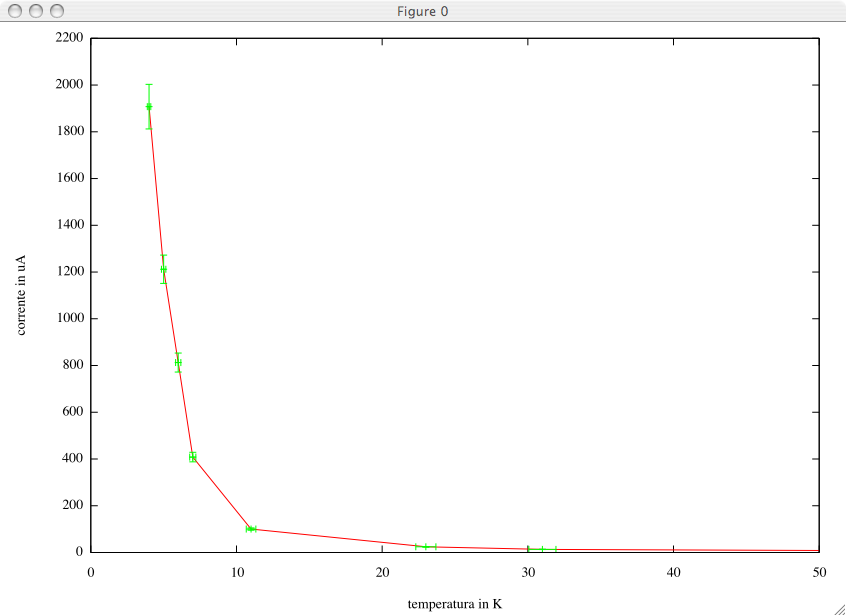
Un esempio di fit di dati sperimentali
Normalmente, il collegare fra loro i diversi punti di misura può servire al pił come una linea per la lettura del grafico, ma può essere pił interessante per esempio realizzare una regressione con una curva teorica, di modo da estrapolare dei dati di un modello. Per esempio, supponiamo che la dipendenza della corrente rispetto alla temperatura nel caso che stiamo considerando segua una legge del tipo 1mA*exp(-b*(x-c))+d, dove b, c e d sono dei parametri pił o meno liberi. Possiamo chiedere a Gnuplot di realizzare un fit basandosi sui dati che abbiamo, per calcolare i valori dei parametri che meglio fanno adattare la curva in questione ai dati sperimentali.
gnuplot> f(x)=exp(-b*(x-c))+d
gnuplot> b=1
gnuplot> c=10
gnuplot> d=0.023
gnuplot> fit f(x) 'data_gnuplot.txt' using ($2):($4) via b,c,d
Iteration 0
WSSR : 4.12945e+06 delta(WSSR)/WSSR : 0
delta(WSSR) : 0 limit for stopping : 1e-05
lambda : 564.399
initial set of free parameter values
b = 1
c = 10
d = 0.023
*/
Iteration 1
WSSR : 2.66856e+06 delta(WSSR)/WSSR : -0.547443
delta(WSSR) : -1.46089e+06 limit for stopping : 1e-05
lambda : 564.399
resultant parameter values
b = 1.12016
c = 10.0214
d = 0.0231075
******** Taglio un bel po' **********
Iteration 86
WSSR : 8506.14 delta(WSSR)/WSSR : -4.18425e-08
delta(WSSR) : -0.000355918 limit for stopping : 1e-05
lambda : 0.000564399
resultant parameter values
b = 0.471138
c = 20.0252
d = 16.6859
After 86 iterations the fit converged.
final sum of squares of residuals : 8506.14
rel. change during last iteration : -4.18425e-08
degrees of freedom (FIT_NDF) : 4
rms of residuals (FIT_STDFIT) = sqrt(WSSR/ndf) : 46.1144
variance of residuals (reduced chisquare) = WSSR/ndf : 2126.54
Final set of parameters Asymptotic Standard Error
======================= ==========================
b = 0.471138 +/- 0.02751 (5.838%)
c = 20.0252 +/- 0.9298 (4.643%)
d = 16.6859 +/- 28.82 (172.7%)
correlation matrix of the fit parameters:
b c d
b 1.000
c -0.998 1.000
d 0.557 -0.590 1.000
gnuplot> plot f(x) title 'Modello teorico', 'data_gnuplot.txt' using \
($2):($4):(temperror*$2):(currerror*$4) title 'Dati sperimentalì with \
xyerrorbars
gnuplot>
Il risultato è quello di una curva che approssima piuttosto bene l'andamento dei dati sperimentali:
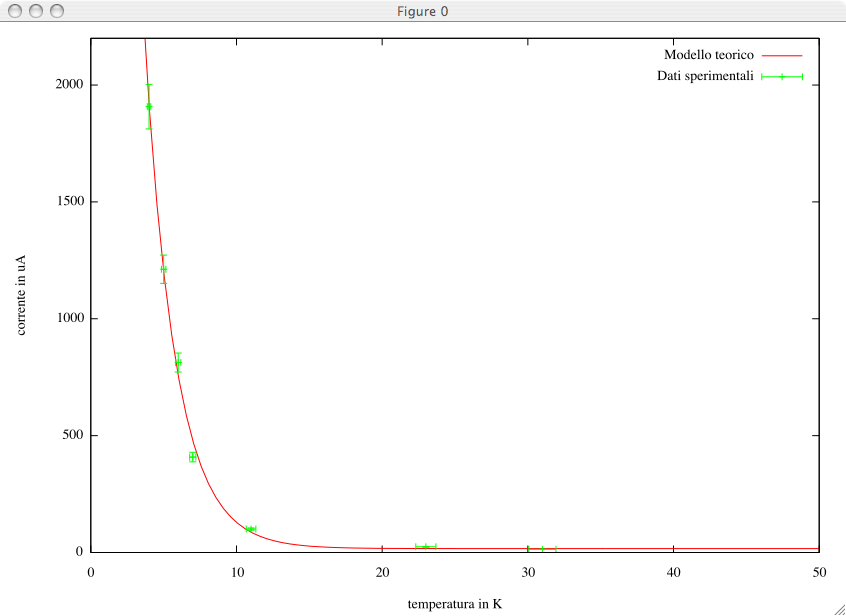
Abbiamo definito una funzione f(x) che dipende da tre parametri, b, c e d ed abbiamo utilizzato il comando fit per ottenere dei valori dei parametri che permettono di far in modo che la curva approssimi ragionevolmente bene i dati sperimentali. E' molto importante la scelta dei valori iniziali dei parametri: il problema è quello di una ricerca di minimo ed una scelta di valori non appropriati per le condizioni iniziali può fare in modo che l'algoritmo di ottimizzazione converga verso una soluzione che NON è quella ottimale. Può essere interessante fare una prova con diverse condizioni iniziali per vedere se si arriva sempre sugli stessi valori dei parametri liberi. Per lo stesso motivo, il comando fit attende di avere un'informazione esplicita (attraverso via) sui parametri che deve prendere in conto per ottimizzare. In molti casi, può essere interessante far variare un parametro alla volta, invece che tutti insieme, per favorire la convergenza.
Un'ultimo appunto. L'apparente facilità d'uso del comando fit non deve far perdere di vista che fare una regressione richiede una buona dose di buon senso, per evitare di prendere fischi per fiaschi. Un'occhiata all'errore standard asintotico può essere utile per rendersi conto dell'affidabilità di alcuni risultati...
Con un buon numero di parametri liberi, si può fare il fit di un elefante...
Dimenticavo, può essere utile utilizzare il comando print per fare qualche calcolo, oppure per ottenere il valore di una variabile.
gnuplot> print b 0.471138066465779 gnuplot> print f(53) 16.6859006122384 gnuplot> print sqrt(500) 22.3606797749979
Nel prossimo paragrafo, parleremo delle tecniche necessarie per ottenere dei file postscript da includere per esempio in un documento LaTeX.
Esportare un grafico in Postscript
Le prime volte che si utilizza Gnuplot, può apparire strano che il programma non preveda dei comandi per stampare, oppure per esportare il grafico che si sta tracciando in un file. In realtà, il meccanismo che Gnuplot adotta per disegnare, e che ruota attorno al concetto di terminale grafico rende il programma molto flessibile sotto questo punto di vista. Esistono infatti diversi terminali grafici che permettono di ottenere dei file contenenti i grafici che ci interessano in diversi formati. Nella nostra discussione, ci interesseremo particolarmente al formato EPS (Encapsulated Postscript), che è vettoriale e si adatta molto bene per ottenere dei grafici da utilizzare all'interno di un file LaTeX, per esempio. Il formato EPS è inoltre adatto ad essere fornito così com'è direttamente in pasto a stampanti laser di buon livello, per avere una stampa su carta con qualità professionale. Il programma Anteprima, sotto MacOSX, normalmente permette di aprire senza problemi un file EPS, che converte all'istante in pdf. Sotto altri sistemi operativi come Linux, può essere utile manipolare i file EPS e PS con Ghostscript e con la suite di programmi che vi ruotano attorno.
Dovendo scrivere un po' di comandi uno dopo l'altro, è opportuno utilizzare un altra caratteristica molto importante di Gnuplot, ovvero gli script. Ci rifaremo all'esempio del fit fornito nell'intervento precedente, solo che questa volta forniremo anche i comandi necessari per ottenere un file EPS pronto per la stampa. Basterà mettere i comandi seguenti in un file, che chiameremo per esempio fit_temperatura.gp. L'estensione del file può essere qualsiasi. A me, piace usare l'estensione .txt per i file che contengono dei dati e l'estensione .gp per gli script di Gnuplot, ma potrete fare come meglio vi aggrada.
# In questo script, effettuiamo un fit su dei dati sperimentali, mostriamo
# il risultato a video e diciamo a Gnuplot di preparare un file EPS pronto
# per la stampa e contenente il grafico.
f(x)=exp(-b*(x-c))+d
b=1
c=10
d=0.023
fit f(x) 'data_gnuplot.txt' using ($2):($4) via b,c,d
temperror=0.03
currerror=0.05
set xrange [0:50]
set yrange [0:2200]
set xlabel 'Temperatura in K'
set ylabel 'Corrente in {/Symbol m}A'
plot f(x) title 'Modello teorico', 'data_gnuplot.txt' using \
($2):($4):(temperror*$2):(currerror*$4) title 'Dati sperimentalì with \
xyerrorbars
# Salviamo il terminale che stiamo usando (Aquaterm) in uno stack
set terminal push
# Impostiamo un terminale postscript
set terminal postscript portrait enhanced mono "Helvetica" 15
# Riduciamo le dimensioni verticali del grafico rispetto ad una pagina A4
set size 1.0, 0.4
# Introduciamo il nome del file che conterrà il grafico
set output "fit_temperatura.eps";
# Ridisegno
replot;
set output
# Ripristino dallo stack del terminale Aquaterm
set terminal pop
# Ripristino della dimensione originale del grafico
set size 1,1
I commenti che ho riportato dovrebbero permettere di capire pił o meno come funziona lo script. Per ottenere l'esecuzione dello script basta essere con Gnuplot nella stessa directory in cui si trovano i file fit_temperatura.gp e data_gnuplot.txt e lanciare l'esecuzione con il comando load:
gnuplot> load 'fit_temperatura.gp'
Gnuplot caricherà i dati, farà il fit, mostrerà il risultato a schermo e creerà il file fit_temperatura.eps che conterrà, se tutto ha funzionato correttamente, il grafico pronto per la stampa, o l'inclusione in un file LaTeX.
Qualche occhio critico avrà notato che nell'intervento precedente avevo rappresentato i microamper con il simbolo uA, utilizzando una u minuscola come surrogato della lettera mu greca. Dato che questo non è accettabile in una stampa di qualità, ho adottato un piccolo trucco che consiste nello scrivere nella legenda dell'asse y il codice Postscript necessario per scrivere la lettera mu. A schermo ovviamente il codice compare tale e quale, ma il file EPS è perfetto. Qui c'è il risultato, in formato EPS e in una versione convertita in PNG. E' ovvio che sul file EPS originale si può ingrandire quanto si vuole ed i dettagli non perdono di definizione, perché si tratta di un file vettoriale, che ha tra l'altro una dimensione di 20 KiB. Se si confronta questo valore con i 48 KiB del file PNG che oltretutto ha una risoluzione non molto elevata, ci si rende conto dell'interesse nell'utilizzare quando possibile una rappresentazione vettoriale di grafici e schemi. Il formato EPS è perfetto per questo.
Un'altro espediente interessante è costituito dallo stack in cui può essere salvato il terminale corrente (munitevi se possibile di una versione recente di Gnuplot per servirvene). Questo è perfetto nel nostro caso, in cui è necessario passare temporaneamente ad un terminale postscript, per poi ristabilire la situazione di partenza.
Durante l'impostazione del terminale, alla linea:
set terminal postscript portrait enhanced mono "Helvetica" 15
abbiamo utilizzato diverse opzioni del terminale postscript. In particolare, abbiamo scelto di utilizzare una versione migliorata del terminale, che permette in particolare di ottimizzare i tratteggi delle diverse curve. Abbiamo scelto (tramite il modificatore mono) una rappresentazione monocromatica. Personalmente, cerco di fare sempre in modo che i grafici che rappresento possano essere interpretati correttamente anche se riprodotti in bianco e nero, cosa che accade di frequente in stampa, in fotocopia eccetera. Ehnanced vuole dire che il terminale riconosce ed interpreta alcune stringhe di comando postscript, per ottenere degli effetti particolari. Trovo molto utile l'apice ^, per ottenere degli esponenti per esempio in certe unità di misura o altro.
Helvetica 15 vuole dire di utilizzare il noto font sans serif Helvetica in corpo 15.
Rappresentazione avanzata di superfici
In questo paragrafo, vedremo alcuni esempi un po' pił avanzati, per rappresentare per esempio delle superfici. Incominciamo con una funzione che è un grande classico di questo genere di esempi (la prima volta che l'ho tracciata è stato utilizzando un VIC-20[1], fate voi...):
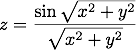
gnuplot> splot sin(sqrt(x*x+y*y))/sqrt(x*x+y*y)
Il risultato è però piuttosto scarno:
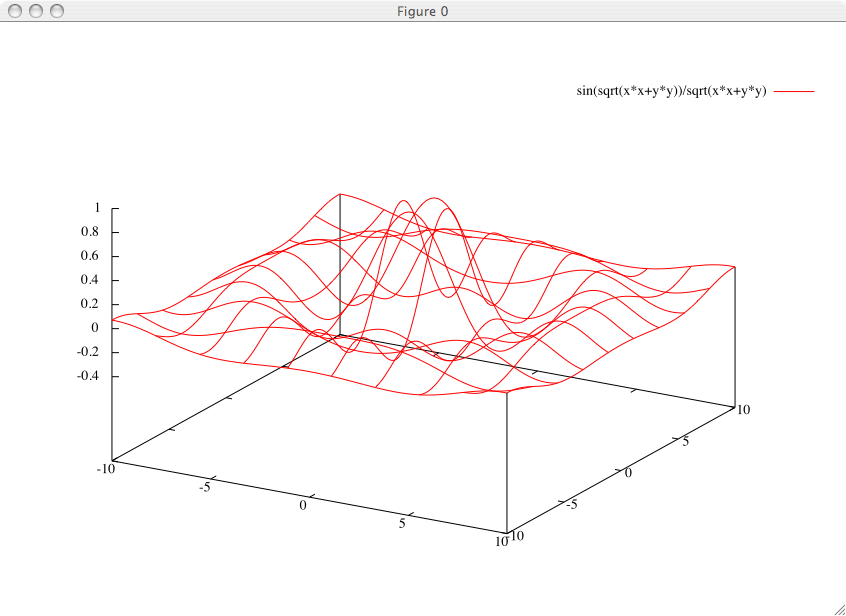
Di default, Gnuplot è configurato per rappresentare delle superfici in wireframe (termine pił o meno traducibile come struttura a fili). Si può scegliere di aumentare la risoluzione con cui la funzione viene tracciata, ovvero il numero di fili utilizzati utilizzando set samples e set isosamples:
gnuplot> set samples 50 gnuplot> set isosamples 50 gnuplot> splot sin(sqrt(x*x+y*y))/sqrt(x*x+y*y) gnuplot>
Una cosa che può migliorare considerevolmente la qualità del risultato tracciato è l'eliminazione delle linee nascoste. In questo modo, la funzione verrà rappresentata tramite una superficie, anche se il disegno prenderà pił tempo per essere tracciato. E' possibile cambiare l'angolo di osservazione della funzione rappresentata in 3D attraverso il comando set view e consultarlo attraverso show view:
gnuplot> show view
view is 60 rot_x, 30 rot_z, 1 scale, 1 scale_z
gnuplot> set view 80, 20,1,1
gnuplot> replot
gnuplot>
Questa vista mette in evidenza il fatto che l'algoritmo di eliminazione delle linee nascoste effettua una distinzione fra il "sopra" ed il "sotto" della superficie, che sono rappresentati in due colori diversi:
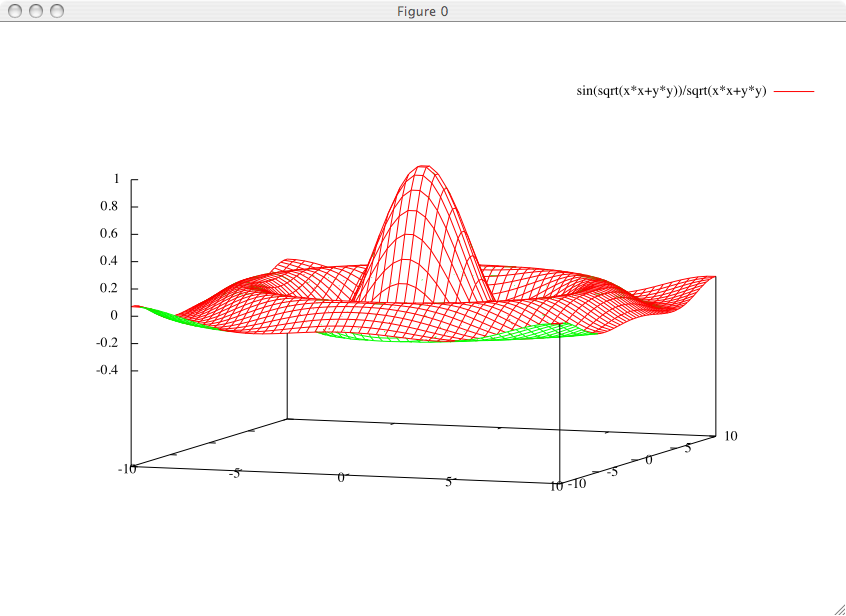
Gnuplot permette di rappresentare oltre alla superficie anche le curve di livello, cosa che è particolarmente comoda in molte situazioni, quando la situazione tende a diventare complicata:
gnuplot> set contour gnuplot> set cntrparam levels discrete 0, 0.125, 0.25, 0.5,0.75, -0.125 gnuplot> replot gnuplot> set contour both gnuplot> replot gnuplot> unset surface gnuplot> replot gnuplot>
Nell'esempio qui sopra, vediamo come Gnuplot può rappresentare delle curve di livello sotto la superficie, oppure sulla superficie, che al limite può non essere tracciata (il controllo avviene tramite i comandi set/unset surface, mentre le linee di livello sono attivate/disattivate con set/unset contour).
Qui ho anche utilizzato set cntrparam per specificare esplicitamente quali livelli desidero tracciare. Le opzioni possibili sono numerose, non parlerò di tutte e consiglio di riferirsi per i dettagli all'help del programma, che è parecchio completo, relativamente comprensibile e con un buon numero di esempi interessanti:
gnuplot> help set cntrparam
`set cntrparam` controls the generation of contours and their smoothness for
a contour plot. `show contour` displays current settings of `cntrparam` as
well as `contour`.
Syntax:
set cntrparam { { linear
| cubicspline
| bspline
| points <n>
| order <n>
| levels { auto { <n>} | <n>
| discrete <z1> {, <z2>{, <z3>...}}
| incremental <start>, <incr> {, <end>}
}
}
}
show contour
This command has two functions. First, it sets the values of z for which
contour points are to be determined (by linear interpolation between data
points or function isosamples.) Second, it controls the way contours are
drawn between the points determined to be of equal z.
********* Qui taglio per brevità *********
Examples:
set cntrparam bspline
set cntrparam points 7
set cntrparam order 10
To select levels automatically, 5 if the level increment criteria are met:
set cntrparam levels auto 5
To specify discrete levels at .1, .37, and .9:
set cntrparam levels discrete .1,1/exp(1),.9
To specify levels from 0 to 4 with increment 1:
set cntrparam levels incremental 0,1,4
To set the number of levels to 10 (changing an incremental end or possibly
the number of auto levels):
set cntrparam levels 10
To set the start and increment while retaining the number of levels:
set cntrparam levels incremental 100,50
See also `set contour` for control of where the contours are drawn, and
`set clabel` for control of the format of the contour labels and linetypes.
Press return for more:
See also
contours demo (contours.dem)
and
contours with user defined levels demo (discrete.dem).
gnuplot>
Nel caso si volessero rappresentare solamente le curve di livello, può risultare pił flessibile fare in modo che Gnuplot le calcoli, immagazzinare i risultati in un file da rappresentare poi in seguito con il comando plot. Riprendo qui un esempio dall'help in linea del programma, che completo e che possiamo memorizzare in uno script di nome livelli.gp:
# Questo script visualizza una funzione z=f(x,y) utilizzando delle curve di # livello. Viene utilizzato un file accessorio chiamato livelli.txt unset surface set contour set samples 100 set isosamples 100 set cntrparam levels discrete 0, 0.125, 0.25, 0.5,0.75, -0.125 set table 'livelli.txt' splot sin(sqrt(x*x+y*y))/sqrt(x*x+y*y) unset table # Le informazioni sulle curve di livello sono in livelli.txt plot 'livelli.txt' with lines notitle
Lo script genera il file accessorio livelli.txt che contiene i dati relativi alle curve di livello desiderate e traccia queste curve solo in un secondo tempo, tramite il comando plot, utilizzando i dati memorizzati nel file.
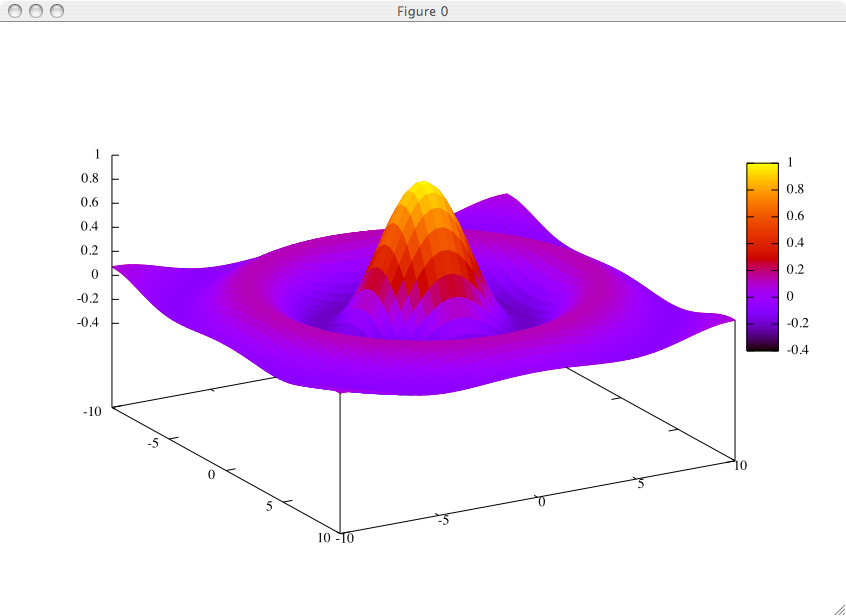
Per terminare, dalla versione 4.0 di Gnuplot è stata aggiunta una rappresentazione tridimensionale molto accattivante graficamente, soprattutto per rappresentare dei dati su un monitor a colori, oppure avendo una stampa di qualità a colori. Si tratta della colorazione della superficie (o meglio, di ogni poligono che la compone) con un colore che dipende dal valore della funzione nel punto. Per attivare questa visualizzazione, si può utilizzare il comando set pm3d:
gnuplot> unset contour gnuplot> set pm3d gnuplot> set surface gnuplot> set view 60,60,1,1 gnuplot> splot sin(sqrt(x*x+y*y))/sqrt(x*x+y*y) notitle gnuplot>
Il cui risultato è il seguente:
[1] - Ho di recente (marzo 2009) ritrovato l'articolo che descriveva come rappresentare la funzione seno cardinale sul VIC-20. E' stato pubblicato nel settembre 1982 su MC microcomputer n. 14, ad opera del grande Andrea de Prisco che l'ha messo fra l'altro a disposizione sul suo sito. Se volete leggervelo, andate nella pagina principale, sotto "Articolografia", cliccate sull'articolo "Grafica senza la scheda".
Conclusioni
Gnuplot è un programma molto potente, capace di produrre dei grafici molto complessi e di qualità estremamente elevata. Tuttavia, si tratta di un programma che necessita un certo periodo di apprendimento per poter conoscere ed apprezzare la filosofia di utilizzo. Spero di aver fornito dei contributi utili scrivendo questa paginetta.License:
--------
Copyright (C) 2007 Davide Bucci davbucci at tiscali dot it
This program is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program; if not, write to the Free Software
Foundation, Inc., 675 Mass Ave, Cambridge, MA 02139, USA.
