Une introduction à Maxima
Le calcul symbolique OpenSource
Quelques exemple pour commencer
Interaction avec Gnuplot
Traiter des expressions trigonométriques
Manipulation sur des polynômes
Un exemple pratique : le test de Hurwitz
Calculs en précision arbitraire
Calcul matriciel et interaction avec TeX
Quelques exemples d'analyse mathématique
Définir une fonction sous Maxima
Conclusion
Introduction
Macsyma a été le premier programme de manipulation symbolique, développé au MIT entre la fin des années soixante et le début des année quatre-vingt du XX siècle. Logiciels tels que Mathematica doivent beaucoup à ces efforts des pionniers.
http://en.wikipedia.org/wiki/Macsyma
Il existe une version open source de Macsyma, sous licence GPL et adaptée au Common Lisp et son nom est Maxima.
http://en.wikipedia.org/wiki/Maxima
J'espère que la traduction de cette page de la version italienne puisse être utile aux navigateurs de la toile française.
Comme beaucoup d'autres outils OpenSource purs et durs (tels que Gnuplot ou Octave), la façon classique d'utiliser Maxima est à l'intérieur d'un terminal. Cet aspect n'est pas gênant pour qui a l'habitude à utiliser des instruments de ce type.
Dans cette présentation, je vais considérer que Maxima a déjà été installé correctement sur votre machine. Pour ce qui me concerne, je me suis servi de plusieurs ordinateurs Apple Macintosh, avec MacOSX.
Cette page a été écrite en assemblant (et en traduisant en français) plusieurs interventions que j'ai faites sur un forum en Italien dédié aux ordinateurs Apple, Macitynet. J'y participe souvent avec le surnom de DarwinNE
![]() http://www.macitynet.it/forum/showthread.php?t=47855
http://www.macitynet.it/forum/showthread.php?t=47855
Quelques exemple pour commencer
Une fois exécuté, Maxima donne le bienvenu et répond avec une invite de commandes :davidebucci@Darwin]$ maxima Maxima 5.11.0 http://maxima.sourceforge.net Using Lisp CLISP 2.38 (2006-01-24) Distributed under the GNU Public License. See the file COPYING. Dedicated to the memory of William Schelter. This is a development version of Maxima. The function bug_report() provides bug reporting information. (%i1)Les lignes identifiées avec %i, suivies par un nombre progressif constituent l'invite de commandes. Maxima dit de cette façon qu'il est prêt à exécuter une commande introduite par l'utilisateur. Une fois la commande exécutée, les résultats de l'exécution sont montrés avec l'écriture %o, suivie par le nombre progressif. Voici un exemple de ce que l'on peut faire facilement avec Maxima ; calculer le factoriel de 300 :
(%i37) 300!; (%o37) 30605751221644063603537046129726862938858880417357699941677674125947653\ 317671686746551529142247757334993914788870172636886426390775900315422684292790\ 697455984122547693027195460400801221577625217685425596535690350678872526432189\ 626429936520457644883038890975394348962543605322598077652127082243763944912012\ 867867536830571229368194364995646049816645022771650018517654646934011222603472\ 972406633325858350687015016979416885035375213755491028912640715715483028228493\ 795263658014523523315693648223343679925459409527682060806223281238738388081704\ 9600000000000000000000000000000000000000000000000000000000000000000000000000 (%i38)
Dans l'exemple que nous venons de voir, j'ai introduit tout simplement 300!; et j'ai confirmé avec un retour à la ligne. Le point virgule indique à Maxima que l'instruction est finie et qu'elle doit être élaborée, avant de passer à la suivante. La barre \ que l'on voit à la fin de la ligne, dans les résultats, indique tout simplement que les résultats continuent sans interruption à la ligne suivante. Le programme calcule très facilement le factoriel de 1000 ou de 10000, mais je ne reporte ici les résultats, car la place occupée par le résultat sera inutilement trop grande.
Voyons par exemple le calcul de la dérivée de sin(x)^5*exp(x) par rapport à x :
(%i38) diff(sin(x)^5*%e^x,x);
x 5 x 4
(%o38) %e sin (x) + 5 %e cos(x) sin (x)
Le logiciel sait traiter correctement la constante de Néper (indiquée avec %e), et la constante pi (%pi).
Voyons le calcul de l'intégrale indéfinie de sin(x)^5 par rapport à x:
(%i39) integrate(sin(x)^5,x);
5 3
cos (x) 2 cos (x)
(%o39) - ------- + --------- - cos(x)
5 3
(%i40)
Pour sortir du logiciel, il suffit de rentrer la commande quit();
(%i1) quit(); [davidebucci@Darwin]$
Interaction avec Gnuplot
Gnuplot est un outil de traçage de graphiques scientifiques très connu soit pour la qualité des résultats, soit par le fait d'être plutôt difficile à maitriser. Maxima peut interagir avec lui de façon plutôt naturelle. Il faut donc disposer d'une version correctement installée de Gnuplot pour profiter de ces possibilités. Dans la page Introduction à Gnuplot, j'ai donné quelques exemples de l'utilisation de Gnuplot. Même s'il n'est pas absolument indispensable de connaître Gnuplot dans les détails pour tracer quelque courbes à l'intérieur de Maxima, il est mieux avoir une idée sur son fonctionnement.
On va commencer avec le graphique d'une fonction simple, telle que sin(x)/x :
(%i1) f: sin(x)/x;
sin(x)
(%o1) ------
x
(%i2) plot2d(f,[x,-3*%pi,3*%pi], [gnuplot_term, aqua]);
Output file "/Users/davidebucci/maxplot.aqua".
(%o2)
(%i3)
Et voici le résultat :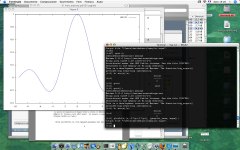
Les dernières versions de Gnuplot permettent d'obtenir des graphiques plutôt élaborés, mais il faut bien connaître ce logiciel. On fera juste un exemple de comment spécifier des commandes Gnuplot à l'intérieur de Maxima, pour obtenir un graphique en trois dimensions :
(%i19) f: sin(sqrt(x^2+y^2));
2 2
(%o19) sin(sqrt(y + x ))
(%i20) plot3d(f,[x,-3*%pi,3*%pi],[y,-3*%pi,3*%pi],[gnuplot_term,aqua], \
[gnuplot_pm3d, true], [gnuplot_preamble,"set pm3d at s;unset surface; \
unset key"]);
Output file "/Users/davidebucci/maxplot.aqua".
(%o20)
(%i21)
Et voici le résultat. Dans mon installation de Gnuplot sous MacOSX, j'utilise le terminal Aqua que j'ai spécifié de façon explicite avec l'option [gnuplot_term,aqua]. Sous d'autres systèmes d'exploitation il peut être judicieux d'adapter le choix du terminal à ce dont vous disposez.
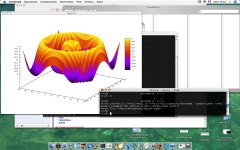
Si vous n'avez pas un terminal graphique, on peut aussi faire en sorte que Gnuplot donne une représentation avec les caractères ASCII. Même si la précision n'est pas très élevée, ces dessins conservent un certain charme d'antan...
(%i21) f: sin(x)/x;
sin(x)
(%o21) ------
x
(%i22) plot2d(f,[x,-3*%pi,3*%pi], [gnuplot_term, dumb]);
1 ++-----+------+------+------+----$$$$$----+------+------+------+-----++
+ + + + + $$ + $$ + + sin(x)/x $$$$$$ +
| $$ $$ |
0.8 ++ $$ $$ ++
| $ $ |
0.6 ++ $ $ ++
| $$ $$ |
| $ $ |
0.4 ++ $$ $$ ++
| $ $ |
0.2 ++ $ $ ++
| $$$$$ $$ $$ $$$$$ |
| $$$$ $$$ $$ $$ $$$ $$$$ |
0 ++$$ $$ $$ $$ $$ $$++
| $$$ $$ $$ $$$ |
-0.2 ++ $$$ $$ $$ $$$ ++
| $$$ $$$ |
+ + + + + + + + + + +
-0.4 ++-----+------+------+------+------+------+------+------+------+-----++
-10 -8 -6 -4 -2 0 2 4 6 8 10
Output file "/Users/davidebucci/maxplot.dumb".
(%o22)
(%i23)
Et, après tout, le comportement de la fonction est facilement visible...
Traiter des expressions trigonométriques
Voici quelques exemple de calcul avec des expressions trigonométriques. Je n'ai jamais réussi à rappeler par coeur les différentes formules (c'est probablement pour cette raison que je préfère utiliser la notation exponentielle). Une bonne occasion pour faire effectuer les calculs à une machine.
Nous allons commencer à définir l'expression de départ sin(x+y)^3, une possible exigence peut être celle d'écrire tout en utilisant seulement des termes en sin() et cos(), avec un argument simple composé seulement par une variable. La commande à utiliser en ce cas est trigexpand :
(%i25) ex: sin(x+y)^3;
3
(%o25) sin (y + x)
(%i26) trigexpand(ex);
3
(%o26) (cos(x) sin(y) + sin(x) cos(y))
Une autre exigence peut être celle de convertir les puissances de fonctions trigonométrique en utilisant les propriétés bien connues, de façon à obtenir une somme de termes qui contiennent seulement sin() ou cos() à la puissance 1 (mais avec des arguments complexes). La commande à utiliser est trigreduce :
(%i27) trigreduce(ex);
3 sin(y + x) - sin(3 (y + x))
(%o27) -----------------------------
4
(%i28)
Quelque chose dont on a besoin parfois quand on a des fonctions de type tangente ou cotangente est de revenir à une expression compacte qui est écrite en utilisant seulement sin() ou cos(). On va donc se servir de la commande trigsimp. Voici un exemple où on reprend aussi les effets des commandes vus précédemment :
(%i29) ex1: sin(x)*tan(2*x)^2;
2
(%o29) sin(x) tan (2 x)
(%i30) trigexpand(ex1);
2
4 sin(x) tan (x)
(%o30) ----------------
2 2
(1 - tan (x))
(%i31) trigreduce(ex1);
2
(%o31) sin(x) tan (2 x)
(%i32) trigsimp(ex1);
2
sin(x) sin (2 x)
(%o32) ----------------
2
cos (2 x)
(%i33)
Il est très laborieux de calculer les intégrales définis ou indéfinis de fonctions trigonométriques. L'intégration d'une fonction comme sin(x)^5 selon x ne présente aucune difficulté conceptuelle, à part le fait qu'il y a un bon nombre de calculs ennuyants à effectuer. Une situation où le calcul automatique peut fonctionner très bien :
(%i33) f: sin(x)^5
;
5
(%o33) sin (x)
(%i34) integrate(f);
Wrong number of arguments to integrate
-- an error. To debug this try debugmode(true);
(%i35) integrate(f,x);
5 3
cos (x) 2 cos (x)
(%o35) - ------- + --------- - cos(x)
5 3
(%i36) trigreduce(%);
- cos(5 x) - 5 cos(3 x) - 10 cos(x) cos(3 x) + 3 cos(x)
(%o36) ----------------------------------- + ------------------- - cos(x)
80 6
(%i37)
Observez comme à la ligne 33 j'ai oublié le point virgule. Maxima ne continue pas jusqu'à quand je ne l'ai pas rentré, même à la ligne suivante. Dans la ligne 34, j'ai par contre oublié de spécifier la variable selon laquelle je veux intégrer. La commande à la ligne 36, comme nous venons de voir, indique d'éliminer les exposants supérieurs à 1. Le symbole % indique d'utiliser comme entrée de la commande, le résultat du dernier calcul effectué.
Il est clair que l'on peut dériver le résultat diff(). Je vais reprendre ici l'expression du début, le sinus à la cinq :
(%i37) diff(f);
4
(%o37) 5 cos(x) sin (x) del(x)
Comme je n'ai pas spécifié la variable selon laquelle je voulais calculer la dérivée, Maxima reste sur le général et utilise la forme del(x) pour indiquer le différentiel de x. En spécifiant que x est la variable selon laquelle dériver, l'ambiguïté est enlevée :
(%i48) diff(sin(x)^5,x);
4
(%o48) 5 cos(x) sin (x)
(%i49)
Manipulation algébrique avec des polynômes
On peut définir un polynôme de degré deux, dont on peut calculer facilement les deux racines (réelles, dans ce cas)
(%i54) p: 3*x^2-5*x+2;
2
(%o54) 3 x - 5 x + 2
(%i55) sol: solve(p=0, x);
2
(%o55) [x = 1, x = -]
3
(%i56)
Si les racines sont complexes, ceci n'est pas un problème très grave pour Maxima, car naturellement ce logiciel peut travailler en champ complexe
(%i65) p: 3*x^2+2*x+2;
2
(%o65) 3 x + 2 x + 2
(%i66) sol: solve(p=0, x);
sqrt(5) %i + 1 sqrt(5) %i - 1
(%o66) [x = - --------------, x = --------------]
3 3
(%i67) solve(p=0, x), numer;
`rat' replaced 4.47213595499958 by 24476/5473 = 4.472135940069432
`rat' replaced 4.47213595499958 by 24476/5473 = 4.472135940069432
(%o67) [x = - 6.090504902856446E-5 (12238 %i + 5473),
x = 6.090504902856446E-5 (12238 %i - 5473)]
(%i68) expand(%);
(%o68) [x = - .7453559900115719 %i - .3333333333333333,
x = .7453559900115719 %i - .3333333333333333]
(%i69)
Comme nous pouvons imaginer, comme le discriminant de l'équation est négatif, nous allons obtenir deux racines complexes conjuguées. Maxima fournit une expression en forme compacte comme résultat des manipulations analytiques. Parfois, on préfère avoir les résultats numériques approchés et pour cette raison, j'ai utilisé à la ligne %i67 le modificateur numer, qui force le programme à fournir les résultats en forme numérique, que j'ai fait écrire sous une forme étendue avec expand. Jusqu'à ici, il y a rien de spécial. Il est beaucoup plus intéressant de calculer toutes les racines d'un polynôme de degré élevé. Ceci n'est pas un problème qui est facilement traitable dans le cas général de façon automatique. Maxima propose la fonction allroots(), qui permet d'effectuer les calculs de façon numérique. Nous pouvons obtenir dans les meilleures conditions 16 chiffres significatives, si le problème n'est pas mal conditionné (chose qui malheureusement arrive souvent).
Voici un exemple de degré 12 (que j'ai repris d'un bouquin de circuits électroniques, qui reporte les résultats aussi) :
%i71) p: 1+2*x^3+2*x^6+2*x^9+x^12;
12 9 6 3
(%o71) x + 2 x + 2 x + 2 x + 1
(%i72) allroots(p=0);
(%o72) [x = .8660254151728854 %i + .5000000152932945,
x = .5000000152932945 - .8660254151728854 %i,
x = .4999999999999991 %i - .8660254037844395,
x = - .4999999999999991 %i - .8660254037844395,
x = .9999999999999994 %i + 5.866392267360735E-16,
x = 5.866392267360735E-16 - .9999999999999994 %i,
x = .8660253923959913 %i + .4999999847067038,
x = .4999999847067038 - .8660253923959913 %i,
x = .5000000000000003 %i + .8660254037844387,
x = .8660254037844387 - .5000000000000003 %i, x = - .9999999683898616,
x = - 1.000000031610135]
(%i73)
En observant les résultats, on peut voir que la précision que l'on obtient est d'environ 7-8 chiffres (il est banal d'observer que x=-1 est solution). Problèmes de ce type ne sont pas banals et il faut toujours se donner les instruments pour contrôler son efficace, par exemple en essayant d'autres méthodes numériques et en confrontant les résultats.
Un exemple pratique : le test de Hurwitz
Les polynômes sont très utilisés dans beaucoup de domaines et leurs propriétés dépendent souvent de la position de leurs racines dans le plan complexe. Malheureusement, comme nous venons de voir, effectuer des calculs avec des polynômes de degré élevé est difficile et en traitant le problème avec des méthodes numériques il y a le risque que les erreurs puissent devenir préoccupants. Très souvent, par exemple dans des problèmes liés aux études de stabilité dans les systèmes linéaires, il suffit d'observer la partie réelle des racines, pour voir si elle est positive, nulle ou négative. Pour un polynôme avec des racines réelles, il suffit d'appliquer la règle des signes de Descartes. Quand les solutions sont complexes, cette règle ne suffit plus et il faut appliquer un test plus compliqué qui est appelé test de Hurwitz.
Le test de Hurwitz est un algorithme purement algébrique qui permet d'observer si un polynôme a toutes ses racines avec partie réelle non positive (polynôme hurwitzien en sens faible), ou négative (polynôme hurwitzien en sens stricte). Nous allons voir ici comment effectuer le test de Hurwitz en utilisant Maxima. Voici le polynôme de départ, tiré toujours de mon bouquin de théorie des réseaux électriques (j'utilise p pour indiquer la pulsation complexe, il faut faire en sorte que ce symbole n'ait pas été utilisé précédemment avec d'autres fonctions) :
(%i95) kill(p);
(%o95) done
(%i96) M(p):=56*p^5+7*p^4+161*p^3+18*p^2+98*p+8;
5 4 3 2
(%o96) M(p) := 56 p + 7 p + 161 p + 18 p + 98 p + 8
(%i97)
J'ai défini M(p) comme une fonction qui dépend de la variable p, grâce à l'opérateur :=
La partie paire d'un polynôme est le polynôme formé par tous les termes avec une puissance de p paire. La partie impaire est celle qui a tous les termes avec puissance de p impaire. Le test de Hurwitz consiste à diviser successivement la partie pair par la partie impair (ou vice versa, selon qui a le degré le plus élevé). A la fin, on obtient normalement un terme de degré 1, plus un reste. L'analyse des restes obtenus à chaque division permet de déterminer si un polynome est hurwitzien ou pas. Nous allons commencer donc à extraire partie paire et impaire d'un polynôme, en appliquant quelques petites propriétés :
(%i105) M(p):=56*p^5+7*p^4+161*p^3+18*p^2+98*p+8;
5 4 3 2
(%o105) M(p) := 56 p + 7 p + 161 p + 18 p + 98 p + 8
(%i106) Pa(p):=1/2*(M(p)+M(-p));
1
(%o106) Pa(p) := - (M(p) + M(- p))
2
(%i107) Di(p):=1/2*(M(p)-M(-p));
1
(%o107) Di(p) := - (M(p) - M(- p))
2
(%i108) expand(Pa(p));
4 2
(%o108) 7 p + 18 p + 8
(%i109) expand(Di(p));
5 3
(%o109) 56 p + 161 p + 98 p
(%i110)
Nous allons continuer maintenant à effectuer les divisions successives. Nous allons diviser Di(p) par Pa(p), car la première a le degré le plus élevé. La fonction à utiliser est divide, qui demande le numérateur, le dénominateur et la variable principale du polynôme.
(%i110) divide(Di(p),Pa(p),p);
3
(%o110) [8 p, 17 p + 34 p]
(%i111)
Le résultat est fourni sous la forme d'une liste, c'est à dire d'une série d'éléments entre crochets, séparés par une virgule. Le premier élément est le résultat de la division, le deuxième est le reste. Le test de Hurwitz consiste à itérer les divisions successives, en ce cas en divisant la partie paire par le reste, qui est impair. On va obtenir le reste en prenant donc le deuxième élément de la liste :
(%i128) Di1(p):=second(%o110);
(%o128) Di1(p) := second(%o110)
(%i129) Di1(p);
3
(%o129) 17 p + 34 p
(%i130) divide(Pa(p), Di1(p),p);
7 p 2
(%o130) [---, 4 p + 8]
17
(%i131)
Nous allons continuer jusqu'à qu'on a plus rien à diviser :
(%i131) Pa1(p):=second(%o130);
(%o131) Pa1(p) := second(%o130)
(%i132) Pa1(p);
2
(%o132) 4 p + 8
(%i133) divide(Di1(p),Pa1(p),p);
17 p
(%o133) [----, 0]
4
(%i134)
En récapitulant, nous avons obtenu comme quotients de premier degré 8p, 7p/17 et 17p/4. Les coefficients de p sont tous positifs, mais ils sont trois au lieu de cinq (c'est à dire le degré du polynôme de départ). Ceci nous permet de conclure que le polynôme M(p) est hurwitzien au sens faible et que toutes ses racines ont donc partie réelle non positive.
Le texte que j'ai utilisé pour les exemples est "Sintesi dei circuiti passivi", de Claudio Beccari édité par CLUT.
Calculs avec précision arbitraire
L'opérateur bfloat() permet de définir tous les éléments de l'expression qui a été fournie comme des big float, c'est à dire des nombres en virgule flottante avec une précision arbitraire. Le numéro de chiffres significatives est défini par la valeur de la variable fpprec. Voici comme l'on peut imprimer les 50000 premières chiffres de la constante pi :
(%i143) fpprec:50000; (%o143) 50000 (%i144) bfloat(%pi); (%o144) 3.1415926535897... Ici, je coupe un peu... ...712307568610450045489703600795698276263923441071465848957802414081584052295\ 369374997106655948944592462866199635563506526234053394391421112718106910522900\ 24657423488b0
J'ai vérifié le résultat avec ce site (qui reporte pi avec 4 millions de chiffres) et le résultat est correcte à l'intérieur de la précision considérée : http://zenwerx.com/pi.php
Calcul matriciel et composition avec TeX
Dans cette partie, nous allons voir brièvement comme on peut faire quelques calculs avec des matrices et comme on peut se servir de TeX pour montrer les résultats.
Voici une des techniques qui peuvent être utilisées pour rentrer une matrice dans le logiciel, la commande entermatrix, qui a besoin de voir spécifiées les dimensions de la matrices :
(%i154) a: entermatrix(4,4);
Is the matrix 1. Diagonal 2. Symmetric 3. Antisymmetric 4. General
Answer 1, 2, 3 or 4 :
4;
Row 1 Column 1:
k^2-1;
Row 1 Column 2:
3
;
Row 1 Column 3:
1;
Row 1 Column 4:
1;
Row 2 Column 1:
5;
Row 2 Column 2:
3;
Row 2 Column 3:
2;
Row 2 Column 4:
1;
Row 3 Column 1:
k;
Row 3 Column 2:
2;
Row 3 Column 3:
1;
Row 3 Column 4:
-1;
Row 4 Column 1:
k;
Row 4 Column 2:
-1;
Row 4 Column 3:
2;
Row 4 Column 4:
0;
Matrix entered.
[ 2 ]
[ k - 1 3 1 1 ]
[ ]
(%o154) [ 5 3 2 1 ]
[ ]
[ k 2 1 - 1 ]
[ ]
[ k - 1 2 0 ]
(%i155)
La première question permet de spécifier le type de matrice et ensuite on rentre les données un élément à la fois. Nous ne sommes pas obligés à rentrer des valeurs numériques, des variables ou des expressions sont parfaitement acceptables. Nous allons représenter le résultat avec TeX :
(%i156) tex(a);
$$\pmatrix{k^2-1&3&1&1\cr 5&3&2&1\cr k&2&1&-1\cr k&-1&2&0\cr }$$
Le code qui se trouve entre les deux dollars $$ est l'expression écrite en format TeX. Pour qui ne connaisse pas TeX et LaTeX, je conseille d'aller faire un tour ici :
http://fr.wikipedia.org/wiki/TeXhttp://fr.wikipedia.org/wiki/LaTeX
Pour ce qui me concerne, j'ai installé sur mon ordinateur la distribution teTeX et j'ai installé des paquets en plus. Sous MacOSX, il existe un petit logiciel très sympa, LaTeXit :
http://ktd.club.fr/programmation/latexit_fr.php
Ce programme (qui nécessite une distribution LaTeX installée correctement) permet d'écrire une équation et effectuer très pratiquement le copie/coller dans des présentations, textes ou sauvegarder l'image générée.
Le seul problème que j'ai rencontré est le fait que le code généré par Maxima suit les vieilles conventions TeX pur et dur et non pas celles plus récentes offertes par LaTeX. En utilisant LaTeXit, j'ai donc du désactiver le paquet amsmath, en éditant le préambule standard, pour éviter des problèmes de compatibilité avec le code produit par Maxima.
De toute façon, voici le résultat :
Eh, oui... TeX et LaTeX actuellement comptent parmi les systèmes qui permettent d'obtenir des équations de qualité typographique très élevée. En utilisant Maxima, on peut à tout moment obtenir automatiquement le code TeX et obtenir une image de l'équation mise parfaitement en forme, sans aucun effort.
Nous allons continuer avec les matrices. Voici le calcul de la matrice inverse, en utilisant la commande invert. Dans beaucoup de cas, il peut être commode de maintenir en facteur commun le déterminant de la matrice, ce que l'on peut faire avec l'option detout :
(%i160) invert(a);
[ 13 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ k - 10 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
(%o160) Col 1 = [ ]
[ - 6 k - 5 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 9 k - 25 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ 12 ]
[ - ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ 2 (k - 1) ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
Col 2 = [ ]
[ 2 ]
[ k + 6 k - 1 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ 5 (k - 1) - 6 k ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ 1 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ 2 (k - 1) + k - 10 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
Col 3 = [ ]
[ 2 ]
[ k - 6 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ - 8 (k - 1) + 3 k + 3 (10 - 2 k) + 5 ]
[ ------------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ 5 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ - 3 (k - 1) - k + 10 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
Col 4 = [ ]
[ 2 ]
[ 5 (k - 1) + 3 k + 3 (- k - 5) - 10 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ - k - 3 k - 3 (5 - 2 k) + 11 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
(%i161)
On peut voir comme le résultat est présenté colonne par colonne. Nous pouvons aussi tester que le produit entre la matrice de départ pour son inverse donne bien la matrice identité :
(%i168) a . b;
[ 2 ]
[ k - 1 3 1 1 ]
[ ]
(%o168) [ 5 3 2 1 ] . (matrix([13, - 12, 1, 5],
[ ]
[ k 2 1 - 1 ]
[ ]
[ k - 1 2 0 ]
2 2 2
[k - 10, 2 (k - 1), 2 (k - 1) + k - 10, - 3 (k - 1) - k + 10],
2 2 2
[- 6 k - 5, k + 6 k - 1, k - 6, 5 (k - 1) + 3 k + 3 (- k - 5) - 10],
2 2
[9 k - 25, 5 (k - 1) - 6 k, - 8 (k - 1) + 3 k + 3 (10 - 2 k) + 5,
2 2
- k - 3 k - 3 (5 - 2 k) + 11])/(13 (k - 1) + 3 k + 3 (k - 10) - 30))
(%i169) c:expand(a . b);
[ 2 ]
[ 13 k 6 k 73 ]
[ ---------------- + ---------------- - ---------------- ]
[ 2 2 2 ]
[ 13 k + 6 k - 73 13 k + 6 k - 73 13 k + 6 k - 73 ]
(%o169) Col 1 = [ ]
[ 0 ]
[ ]
[ 0 ]
[ ]
[ 0 ]
[ 0 ]
[ ]
[ 2 ]
[ 13 k 6 k 73 ]
[ ---------------- + ---------------- - ---------------- ]
Col 2 = [ 2 2 2 ]
[ 13 k + 6 k - 73 13 k + 6 k - 73 13 k + 6 k - 73 ]
[ ]
[ 0 ]
[ ]
[ 0 ]
[ 0 ]
[ ]
[ 0 ]
[ ]
[ 2 ]
Col 3 = [ 13 k 6 k 73 ]
[ ---------------- + ---------------- - ---------------- ]
[ 2 2 2 ]
[ 13 k + 6 k - 73 13 k + 6 k - 73 13 k + 6 k - 73 ]
[ ]
[ 0 ]
[ 0 ]
[ ]
[ 0 ]
[ ]
[ 0 ]
Col 4 = [ ]
[ 2 ]
[ 13 k 6 k 73 ]
[ ---------------- + ---------------- - ---------------- ]
[ 2 2 2 ]
[ 13 k + 6 k - 73 13 k + 6 k - 73 13 k + 6 k - 73 ]
(%i170)
L'opérateur produit matriciel est le point. Nous n'avons pas obtenu à première vue la matrice identité, parce que les termes ne sont pas factorisés. Essayons donc d'appliquer la commande factor :
(%i174) factor(c);
[ 1 0 0 0 ]
[ ]
[ 0 1 0 0 ]
(%o174) [ ]
[ 0 0 1 0 ]
[ ]
[ 0 0 0 1 ]
(%i175)
Naturellement, on peut calculer facilement les valeurs propres (eigenvalues en Anglais) ou les vecteurs propres (eigenvectors) avec les commandes eigenvectors(a) et eigenvalues(a), mais je ne vais pas montrer les résultats, car ils prennent beaucoup de place.
Pour terminer, voici un exemple d'une autre expression obtenue grâce à TeX, une intégrale indéfinie :
(%i187) i:'integrate((x^2+2*x+1)/(x-2),x);
/ 2
[ x + 2 x + 1
(%o187) I ------------ dx
] x - 2
/
(%i188) o:integrate((x^2+2*x+1)/(x-2),x);
2
x + 8 x
(%o188) 9 log(x - 2) + --------
2
(%i189) tex(i=o);
$$\int {{{x^2+2\,x+1}\over{x-2}}}{\;dx}=9\,\log \left(x-2\right)+{{x^2
+8\,x}\over{2}}$$
(%o189) false
(%i190)
Dans cet exemple, j'ai utilisé la commande integrate deux fois. La première a été utilisée pour calculer la primitive, tandis que la deuxième fois j'ai tout simplement fait écrire l'expression. J'ai utilisé l'opérateur ' (apostrophe), qui empêche à Maxima d'exécuter l'opération, mais la laisse non élaborée. Je m'en sers pour obtenir le code TeX correspondant. Voici le résultat :
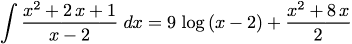
(d'ailleurs... l'égalité est vraie, mais dans le cas général nous avons besoin d'une constante additive).
P.S. Dans la dernière image obtenue avec TeX, je vois un petit bogue. Selon les normes internationales, la 'd' du différentiel ne doit pas être en italique, mais en rond. De toute façon, il s'agit d'une erreur que j'ai trouvée aussi dans des publications. Pour le corriger, il suffit de substituer à la main 'd' avec l'expression {\rm d}.
Quelques exemple d'analyse
Nous avons déjà vi que Maxima n'a pas de problèmes à calculer primitives et dérivées :
(%i194) f:sin(x)/(atan(x)+x^2);
sin(x)
(%o194) ------------
2
atan(x) + x
(%i195) g:diff(f,x);
1
(------ + 2 x) sin(x)
2
cos(x) x + 1
(%o195) ------------ - ---------------------
2 2 2
atan(x) + x (atan(x) + x )
(%i196) 'integrate(g,x)=integrate(g,x);
1
(------ + 2 x) sin(x)
/ 2
[ cos(x) x + 1
(%o196) I (------------ - ---------------------) dx =
] 2 2 2
/ atan(x) + x (atan(x) + x )
cos(x) sin(2 x) - sin(x) cos(2 x) + sin(x)
-------------------------------------------------------
2 2 2 2
(2 atan(x) + 2 x ) sin (x) + (2 atan(x) + 2 x ) cos (x)
(%i197) 'integrate(g,x)=trigreduce(integrate(g,x));
1
(------ + 2 x) sin(x)
/ 2
[ cos(x) x + 1 sin(x)
(%o197) I (------------ - ---------------------) dx = ------------
] 2 2 2 2
/ atan(x) + x (atan(x) + x ) atan(x) + x
(%i198) tex(%);
$$\int {{{\cos x}\over{\arctan x+x^2}}-{{\left({{1}\over{x^2+1}}+2\,x
\right)\,\sin x}\over{\left(\arctan x+x^2\right)^2}}}{\;dx}={{\sin x
}\over{\arctan x+x^2}}$$
(%o198) false
(%i199)
J'ai extrait le code TeX à la ligne %o198,ce qui donne comme résultat :
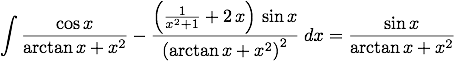
(avec la constante arbitraire qui manque pour le cas général...).
Naturellement, on peut aussi calculer des limites avec la commande limit.
Nous commençons avec une limite classique, la limite pour x qui tend vers zéro de k*sin(x)/x (qui donne k, bien évidemment).
(%i202) f:k*sin(x)/x;
k sin(x)
(%o202) --------
x
(%i203) limit(f,x,0);
(%o203) k
(%i204)
Voyons quelques exemple avec la fonction tangente :
(%i3) limit(tan(x),x,%pi/2); (%o3) und (%i4) limit(tan(x),x,%pi/2,plus); (%o4) minf (%i5) limit(tan(x),x,%pi/2,minus); (%o5) inf
Dans le premier cas, j'ai calculé la limite de la tangente pour x qui tend vers pi/2. Maxima répond correctement que cette limite n'existe pas (und correspond à undefined).
J'ai donc calculé les limites à la droite et à la gauche du même point singulier, en obtenant moins infini (minf) et plus infini (inf).
Les limites sont calculées en utilisant des substitutions qui à la fin donnent une forme qui permet de se référer à une librairie de limites classiques, ou à une confrontation des ordres d'infini/infinitième. Le manuel de Maxime donne comme référence une thèse très intéressante sur l'argument :
http://www.lcs.mit.edu/publications/specpub.php?id=660
D'ailleurs, le directeur de thèse a été Seymour Papert, l'inventeur du LOGO.
Il existe aussi la fonction tlimit(), qui calcule les limites en adoptant un développement limité à l'aide des séries de Taylor ou de Laurent.
Il faut néanmoins faire attentions dans certains cas où la fonction a un comportement pathologique. Voici un exemple :
(%i58) p:(log(1+%e^(1/x))*sin(x^7))/((1/(1-x^2))^(sin(x)^2)-1-x^4);
7 1/x
sin(x ) log(%e + 1)
(%o58) ------------------------
1 4
--------------- - x - 1
2
2 sin (x)
(1 - x )
(%i59) limit(factor(p(x)),x,0,minus);
^CMaxima encountered a Lisp error:
EXT:GC: User break
Automatically continuing.
To reenable the Lisp debugger set *debugger-hook* to nil.
(%i60) limit(factor(p(x)),x,0,plus);
2 2
sin (x) log(1 - x ) 7 1/x
%e sin(x ) log(%e + 1)
(%o60) - limit --------------------------------------------
x -> 0+ 2 2
4 2 sin (x) 2 sin (x)
x (1 - x ) + (1 - x ) - 1
(%i61) tlimit(factor(p(x)),x,0,plus);
(%o61) 0
(%i62) tlimit(factor(p(x)),x,0,minus);
(%o62) 0
(%i63)
Quand j'ai lancé la commande limit(factor(p(x)),x,0,minus);, Maxima a continué à travailler jusqu'à quand j'en ai eu marre et je l'ai interrompu avec CTRL-C.
La commande tlimit semble donner moins de problèmes et fournit zéro presque tout de suite, par contre, ce résultat est faux !
La limite pour x qui tend vers zéro du côté positif de la fonction que j'ai fourni est en fait 6. On peut le démontrer en développant en série de Taylor à un ordre plus élevé de ce qui se fait d'habitude. De toute façon, cette fonction a un comportement plutôt pathologique aux alentours de l'origine, comme on peut voir sur son graphique :
(%i80) plot2d(p(x), [x, -0.1,.1], [gnuplot_term, aqua]);
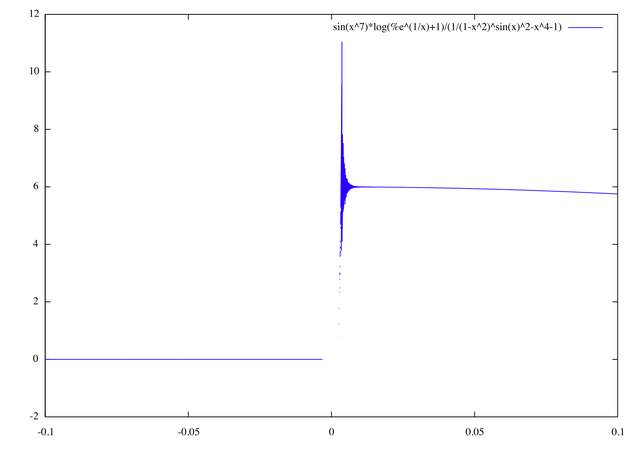
Une possibilité dans ces cas (à utiliser toujours avec attention) est la commande taylor, qui permet, comme son nom indique, de développer une expression selon Taylor ou Laurent aux alentours d'un point singulier, jusqu'à un ordre donné. Le manuel de Maxima reporte :
taylor (expr, x, a, n) expands the expression expr in a truncated Taylor or Laurent series in the variable x around the point a, containing terms through (x - a)^n.Voici un exemple, appliqué à notre cas :
(%i81) p:(log(1+%e^(1/x))*sin(x^7))/((1/(1-x^2))^(sin(x)^2)-1-x^4);
7 1/x
sin(x ) log(%e + 1)
(%o81) ------------------------
1 4
--------------- - x - 1
2
2 sin (x)
(1 - x )
(%i82) taylor(p(x),x,0,1);
(%o82)/T/ 0 + . . .
(%i83) taylor(p(x),x,0,2);
(%o83)/T/ 0 + . . .
(%i84) taylor(p(x),x,0,3);
(%o84)/T/ 0 + . . .
(%i85) taylor(p(x),x,0,4);
(%o85)/T/ 0 + . . .
(%i86) taylor(p(x),x,0,5);
(%o86)/T/ 0 + . . .
(%i87) taylor(p(x),x,0,6);
6
(%o87)/T/ x + . . .
(%i88) taylor(p(x),x,0,7);
2 4 6
128 x 51209 x 2021759 x
(%o88)/T/ 6 - ------ + -------- - ---------- + . . .
5 525 5250
3 5 7
128 x 51209 x 2021759 x - 1/x
+ (6 x - ------ + -------- - ---------- + . . .) %e
5 525 5250
3 5 7
64 x 51209 x 2021759 x - 1/x 2
+ (- 3 x + ----- - -------- + ---------- + . . .) (%e )
5 1050 10500
3 5 7
128 x 51209 x 2021759 x - 1/x 3
+ (2 x - ------ + -------- - ---------- + . . .) (%e )
15 1575 15750
3 5 7
3 x 32 x 51209 x 2021759 x - 1/x 4
+ (- --- + ----- - -------- + ---------- + . . .) (%e )
2 5 2100 21000
3 5 7
6 x 128 x 51209 x 2021759 x - 1/x 5
+ (--- - ------ + -------- - ---------- + . . .) (%e )
5 25 2625 26250
3 5 7
64 x 51209 x 2021759 x - 1/x 6
+ (- x + ----- - -------- + ---------- + . . .) (%e )
15 3150 31500
3 5 7
6 x 128 x 51209 x 2021759 x - 1/x 7
+ (--- - ------ + -------- - ---------- + . . .) (%e ) + . . .
7 35 3675 36750
(%i89)
On obtient un résultat utilisable seulement quand on force le calcul du polynôme de Taylor au moins jusqu'au septième degré. La raison pour laquelle on reporte les termes exponentiels qui n'ont pas été développés est due au fait que e^(1/x) est un objet à traiter avec un certain respect aux alentours de l'origine. Effectivement, on peut remarquer que cette dernière expression est égale à 6 pour x réel qui tend vers zéro du côté positif.
J'ai écrit ces commentaires pour montrer comme, même en utilisant des instruments automatiques, il faut toujours faire très attention et il faut connaître bien le coeur du problème avant même de l'aborder à l'ordinateur. En reprenant une phrase de quelqu'un que je connais, pour utiliser un logiciel de calcul symbolique, il faut savoir faire les calculs mieux que lui.
Définir une fonction en Maxima
On peut définir des fonctions et des commandes qui peuvent être utilisé de façon tout à fait similaire à celles qui sont définies par le programme. Il y a deux techniques qui permettent de faire ceci :
- écrire des macrofonctions en adoptant la syntaxe de Maxima
- écrire des fonctions en Lisp
Nous allons fournir un petit exemple de fonction plutôt complète, écrite en utilisant les commandes de Maxima. L'objectif est celui de rendre automatique le test de Hurwitz que l'on a traité précédemment. Voici le code :
/* Perform the Hurwitz test on the M(p) polynomials using Maxima
Version 1.0
Written by Davide Bucci, March-April 2007
This program is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program; if not, write to the Free Software
Foundation, Inc., 51 Franklin St, Fifth Floor, Boston, MA 02110-1301 USA
*/
/* Exemples de polynome hurwitzien ou pas
-----------------------------------------------
56*p^5+7*p^4+161*p^3+18*p^2+98*p+8, Hurwitzien au sens faible
p^3+2*p^2+4*p+3, Hurwitzien au sens stricte
p^5+2*p^4+2*p^3+4*p^2+11*p+10, Non hurwitzien
p^3+2*p^2+4*p+9, Non hurwitzien
*/
hurwitz(poly,var):=block ([M,p],
/* On définit ici une fonction qui va nous permettre de travailler
sur notre polynôme de façon générale, en utilisant la variable 'var' */
define(M(var),poly),
if(debugmode) then print(M(p)),
print("Test de Hurwitz pour un polynôme"),
/* Calcul de la partie paire et impaire du polynôme */
Pa(p):=expand(1/2*(M(p)+M(-p))),
Di(p):=expand(1/2*(M(p)-M(-p))),
/* Il faut avoir au numérateur la partie qui a le degré le plus élevé */
pg:hipow(Pa(p), p),
dg:hipow(Di(p), p),
num:Di(p),
den:Pa(p),
nm:dg,
if (pg>dg) then
(num:Pa(p), den:Di(p), nm:pg),
if (den#0) then (
res:divide(num,den,p),
/* Cycle des divisions successives */
hasdivided: (second(res)#0),
print(hasdivided),
/* This list will contain the results of the successive divisions */
reslist:[],
ishurwitz:true,
print("Calcul des divisions successives."),
for i:0 thru nm while (hasdivided and ishurwitz) do (
if(debugmode) then (
print("Nouvelle itération"),
print(i),
print("diviser"),
print(num),
print("pour"),
print(den)
),
res:divide(num,den,p),
if(debugmode) then (
print("resultat"),
print(res)
),
hasdivided: (second(res)#0),
reslist:append(reslist,[first(res)]),
num:expand(den),
den:second(res),
/* On voit si le résultat de la division est un monôme de degré 1 avec
coefficient positif */
if (hipow(first(res),p)>1) then (
ishurwitz:false
),
if (coeff(first(res),p,1)<0) then (
ishurwitz:false
)
),
if (length(reslist)=nm and ishurwitz) then
print("Polynome hurwitzien au sens stricte")
elseif (ishurwitz) then
print("Polynome hurwitzien au sens faible")
else
print("Polynome non hurwitzien"),
print(reslist),
reslist
) else
print("Polynome seulement pair ou impair")
)$
Par rapport à l'utilisation normale de Maxima à travers la ligne de commande, nous voyons dans la fonctions des différences. Celle qui saute le plus aux yeux est l'utilisation de la virgule pour séparer les différentes instructions, au lieu du point virgule.
Nous allons placer cette fonction dans un fichier que l'on pourra appeler Hurwitz.max dans le répertoire courant. Pour faire en sorte que Maxima puisse charger la fonction, il faut utiliser la commande load, en indiquant le nom du fichier. Ensuite, on pourra accéder à la fonction hurwitz(pol, var), que l'on va utiliser dans l'exemple qui suit :
(%i5) load("Hurwitz.max");
(%o5) Hurwitz.max
(%i6) hurwitz(56*p^5+7*p^4+161*p^3+18*p^2+98*p+8,p);
Test de Hurwitz pour un polynome
3
17 p + 34 p # 0
Calcul des divisions successives.
Polynôme hurwitzien au sens faible
7 p 17 p
[8 p, ---, ----]
17 4
7 p 17 p
(%o6) [8 p, ---, ----]
17 4
(%i7)
Conclusion
Avec cet article, plus que fournir une description systématique des possibilités considérables offertes par Maxima, l'ai essayé de donner une collection d'exemples avec des commentaires. J'espère que ces exemples puissent donner une inspiration, mais je n'ai fait que effleurer un monde très vaste et très fascinant. Bonne recherche...License:
--------
Copyright (C) 2007-2008 Davide Bucci davbucci at tiscali dot it
This program is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program; if not, write to the Free Software
Foundation, Inc., 675 Mass Ave, Cambridge, MA 02139, USA.
