Un'introduzione a Maxima
Il calcolo simbolico OpenSource
Qualche esempio per incominciare
Interazione con Gnuplot
Trattare espressioni trigonometriche
Manipolazione algebrica su polinomi
Un esempio pratico: la prova di Hurwitz
Calcoli con precisione arbitraria
Calcolo matriciale e composizione con TeX
Qualche esempio di analisi
Definire una funzione in Maxima
Conclusioni
Introduzione
Macsyma è stato il primo programma di manipolazione algebrica sviluppato al MIT fra la fine degli anni sessanta e gli inizi degli anni ottanta. Programmi tipo Mathematica devono molto a questi pioneristici sforzi.
http://en.wikipedia.org/wiki/Macsyma
Ne esiste una versione OpenSource rilasciata secondo la licenza GPL, chiamata Maxima, ed adattata a Common Lisp.
http://en.wikipedia.org/wiki/Maxima
Spero di fare cosa gradita agli utenti italiani descrivendone un po' le funzioni.
Come tanti programmi OpenSource puri e duri (come Gnuplot e Octave), si usa da terminale, a me la cosa non dispiace affatto perché sono abituato ad usare strumenti del genere e quasi tutti i miei file di lavoro (testo puro) sono così compatibili con qualunque ambiente e sistema operativo.
In questa presentazione, supporrò che il programma sia stato installato correttamente. Nel mio caso, l'ho usato efficacemente su diversi Apple Macintosh, sotto MacOSX.
Questa pagina è stata scritta assemblando diversi miei interventi sul forum di Macitynet, a cui partecipo spesso con lo pseudonimo di DarwinNE:
![]() http://www.macitynet.it/forum/showthread.php?t=47855
http://www.macitynet.it/forum/showthread.php?t=47855
Qualche esempio per incominciare
Una volta lanciato, Maxima si presenta come segue:davidebucci@Darwin]$ maxima Maxima 5.11.0 http://maxima.sourceforge.net Using Lisp CLISP 2.38 (2006-01-24) Distributed under the GNU Public License. See the file COPYING. Dedicated to the memory of William Schelter. This is a development version of Maxima. The function bug_report() provides bug reporting information. (%i1)Le linee identificate con %i seguite da un numero progressivo sono il prompt dei comandi, ovvero il modo che Maxima ha per segnalare all'utilizzatore che aspetta che lui introduca un comando. I risultati dell'elaborazione sono identificate con la dicitura %o, seguita dal solito numero progressivo. Ecco un esempio di quello che Maxima può fare, il fattoriale di 300:
(%i37) 300!; (%o37) 30605751221644063603537046129726862938858880417357699941677674125947653\ 317671686746551529142247757334993914788870172636886426390775900315422684292790\ 697455984122547693027195460400801221577625217685425596535690350678872526432189\ 626429936520457644883038890975394348962543605322598077652127082243763944912012\ 867867536830571229368194364995646049816645022771650018517654646934011222603472\ 972406633325858350687015016979416885035375213755491028912640715715483028228493\ 795263658014523523315693648223343679925459409527682060806223281238738388081704\ 9600000000000000000000000000000000000000000000000000000000000000000000000000 (%i38)Nell'esempio sopra, ho introdotto 300!; ed ho premuto invio. Il punto e virgola indica a Maxima che l'istruzione è finita e che va elaborata prima di passare alla successiva. La barra \ che compare a fine riga indica semplicemente che l'output continua nella riga successiva, da considerare senza soluzione di continuità. Il programma calcola senza fare una piega il fattoriale di 1000 e di 10000, solo che prendono troppo spazio ed ho pensato che fosse inutile ingombrare inutilmente questa paginetta. Vediamo per esempio la derivata di sin(x)^5*exp(x) rispetto ad x:
(%i38) diff(sin(x)^5*%e^x,x);
x 5 x 4
(%o38) %e sin (x) + 5 %e cos(x) sin (x)
Il programma sa come trattare la costante di Nepero (indicata con %e), oltre a naturalmente il pi greco (%pi).
Integrale indefinito di sin(x)^5 rispetto ad x:
(%i39) integrate(sin(x)^5,x);
5 3
cos (x) 2 cos (x)
(%o39) - ------- + --------- - cos(x)
5 3
(%i40)
Per uscire dal programma, basta battere quit();
(%i1) quit(); [davidebucci@Darwin]$
Interazione con Gnuplot
Gnuplot è un bel programma di tracciamento, noto sia per la qualità dei grafici assolutamente professionale che può fornire, sia per il fatto di essere piuttosto ostico. Maxima vi si interfaccia in maniera piuttosto naturale. Pertanto, Gnuplot va installato e configurato se si desidera approfittare di questa possibilità. In questa pagina, ho raccolto alcuni esempi relativi all'uso di Gnuplot come programma a sè stante. Pur non essendo indispensabile conoscerlo in dettaglio, può risultare comodo avere comunque un'idea del suo funzionamento per potersene servire dentro Maxima.
Iniziamo con il disegno di una funzione semplice, tipo sin(x)/x:
(%i1) f: sin(x)/x;
sin(x)
(%o1) ------
x
(%i2) plot2d(f,[x,-3*%pi,3*%pi], [gnuplot_term, aqua]);
Output file "/Users/davidebucci/maxplot.aqua".
(%o2)
(%i3)
Ed ecco il risultato: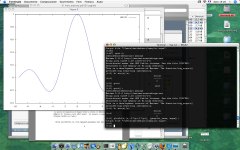
Naturalmente, le ultime versioni di Gnuplot permettono di fare grafici piuttosto complessi, ma bisogna conoscerlo a fondo e non ne parleremo qui in maniera dettagliata. Ecco però un esempio di come specificare dei comandi Gnuplot all'interno di Maxima per ottenere un grafico tridimensionale:
(%i19) f: sin(sqrt(x^2+y^2));
2 2
(%o19) sin(sqrt(y + x ))
(%i20) plot3d(f,[x,-3*%pi,3*%pi],[y,-3*%pi,3*%pi],[gnuplot_term,aqua], \
[gnuplot_pm3d, true], [gnuplot_preamble,"set pm3d at s;unset surface; \
unset key"]);
Output file "/Users/davidebucci/maxplot.aqua".
(%o20)
(%i21)
Ed ecco il risultato. Nella mia installazione di Gnuplot sotto MacOSX, quando ho elaborato questi esempi, il programma partiva senza avere un terminale grafico definito e dovevo quindi specificarlo ogni volta con l'opzione [gnuplot_term,aqua]. Su altre installazioni (per esempio usando altri sistemi operativi) può essere conveniente non utilizzare questa opzione.
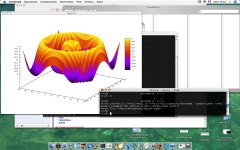
Se proprio non si riesce a configurare un terminale grafico, si può benissimo usare una rappresentazione testuale che, seppure poco attrattiva a primo acchito, conserva tuttavia un certo suo fascino vintage:
(%i21) f: sin(x)/x;
sin(x)
(%o21) ------
x
(%i22) plot2d(f,[x,-3*%pi,3*%pi], [gnuplot_term, dumb]);
1 ++-----+------+------+------+----$$$$$----+------+------+------+-----++
+ + + + + $$ + $$ + + sin(x)/x $$$$$$ +
| $$ $$ |
0.8 ++ $$ $$ ++
| $ $ |
0.6 ++ $ $ ++
| $$ $$ |
| $ $ |
0.4 ++ $$ $$ ++
| $ $ |
0.2 ++ $ $ ++
| $$$$$ $$ $$ $$$$$ |
| $$$$ $$$ $$ $$ $$$ $$$$ |
0 ++$$ $$ $$ $$ $$ $$++
| $$$ $$ $$ $$$ |
-0.2 ++ $$$ $$ $$ $$$ ++
| $$$ $$$ |
+ + + + + + + + + + +
-0.4 ++-----+------+------+------+------+------+------+------+------+-----++
-10 -8 -6 -4 -2 0 2 4 6 8 10
Output file "/Users/davidebucci/maxplot.dumb".
(%o22)
(%i23)
E dopotutto, il comportamento della funzione è interpretabile...
Trattare espressioni trigonometriche
Ecco qualche esempio di calcolo con espressioni trigonometriche. Io non mi sono mai ricordato a memoria le varie equivalenze (sarà per quello che ho poi trovato molto comoda la notazione esponenziale). Una buona occasione per far fare i calcoli ad una macchina.
Iniziamo con il definire l'espressione di partenza: sin(x+y)^3, una possibile esigenza può esser quella di scrivere tutto utilizzando dei termini in sin() e cos(), con argomento semplice composto solo da una variabile. Il comando da utilizzare è trigexpand:
(%i25) ex: sin(x+y)^3;
3
(%o25) sin (y + x)
(%i26) trigexpand(ex);
3
(%o26) (cos(x) sin(y) + sin(x) cos(y))
Un'altra esigenza può essere quella di convertire le potenze di funzioni trigonometriche utilizzando le note proprietà, di modo da ottenere una somma di termini che contengono solo un sin() o cos(), alla potenza 1, però con argomenti più complessi. La funzione da utilizzare è trigreduce:
(%i27) trigreduce(ex);
3 sin(y + x) - sin(3 (y + x))
(%o27) -----------------------------
4
(%i28)
Una cosa che capita alle volte è avere delle funzioni tipo tangente, cotangente ed altro che si desidera riportare in una espressione compatta utilizzando solo seni e coseni. La funzione è trigsimp. Ecco un esempio in cui si vedono anche gli effetti dei comandi visti in precedenza.
(%i29) ex1: sin(x)*tan(2*x)^2;
2
(%o29) sin(x) tan (2 x)
(%i30) trigexpand(ex1);
2
4 sin(x) tan (x)
(%o30) ----------------
2 2
(1 - tan (x))
(%i31) trigreduce(ex1);
2
(%o31) sin(x) tan (2 x)
(%i32) trigsimp(ex1);
2
sin(x) sin (2 x)
(%o32) ----------------
2
cos (2 x)
(%i33)
Quanto è noioso calcolare gli integrali definiti o indefiniti di funzioni trigonometriche... Integrare un seno alla quinta non presenta nessuna difficoltà concettuale, a parte lo svolgere i calcoli. Che sono noiosi. Adatti quindi ad essere eseguiti in maniera automatica:
(%i33) f: sin(x)^5
;
5
(%o33) sin (x)
(%i34) integrate(f);
Wrong number of arguments to integrate
-- an error. To debug this try debugmode(true);
(%i35) integrate(f,x);
5 3
cos (x) 2 cos (x)
(%o35) - ------- + --------- - cos(x)
5 3
(%i36) trigreduce(%);
- cos(5 x) - 5 cos(3 x) - 10 cos(x) cos(3 x) + 3 cos(x)
(%o36) ----------------------------------- + ------------------- - cos(x)
80 6
(%i37)
Si noti come nell'input 33 ho dimenticato il punto e virgola. Maxima non continua fintantoché non l'inserisco, per esempio nella riga successiva. Nell'input 34 ho invece dimenticato la variabile secondo cui integrare. Il comando alla linea 36 come visto sopra indica invece di eliminare le potenze ed ottenere delle somme in cui le funzioni trigonometriche compaiono solo con potenza 1. Il simbolo di percento % indica di utilizzare nel processo l'ultimo risultato ottenuto.
Ovviamente, si può derivare, con il comando diff(). Riprendo qui l'espressione iniziale, il seno alla quinta:
(%i37) diff(f);
4
(%o37) 5 cos(x) sin (x) del(x)
In questo caso, non avendo specificato la variabile secondo cui differenziare, Maxima resta sul generale e la forma del(x) indica appunto il differenziale di x. Volendo dire di differenziare rispetto ad x, non c'è più quest'ambiguità:
(%i48) diff(sin(x)^5,x);
4
(%o48) 5 cos(x) sin (x)
(%i49)
Manipolazione algebrica su polinomi
Definiamo un polinomio per esempio di grado due, di cui possiamo estrarre facilmente le due radici (reali):
(%i54) p: 3*x^2-5*x+2;
2
(%o54) 3 x - 5 x + 2
(%i55) sol: solve(p=0, x);
2
(%o55) [x = 1, x = -]
3
(%i56)
Se le radici non sono reali, questo non costituisce un gran problema per Maxima, dato che naturalmente si può lavorare in campo complesso:
(%i65) p: 3*x^2+2*x+2;
2
(%o65) 3 x + 2 x + 2
(%i66) sol: solve(p=0, x);
sqrt(5) %i + 1 sqrt(5) %i - 1
(%o66) [x = - --------------, x = --------------]
3 3
(%i67) solve(p=0, x), numer;
`rat' replaced 4.47213595499958 by 24476/5473 = 4.472135940069432
`rat' replaced 4.47213595499958 by 24476/5473 = 4.472135940069432
(%o67) [x = - 6.090504902856446E-5 (12238 %i + 5473),
x = 6.090504902856446E-5 (12238 %i - 5473)]
(%i68) expand(%);
(%o68) [x = - .7453559900115719 %i - .3333333333333333,
x = .7453559900115719 %i - .3333333333333333]
(%i69)
Come ci aspettavamo, dato che il discriminante è negativo, si ottengono le due radici complesse e coniugate. Maxima fornisce un'espressione in forma compatta resultante dalle manipolazioni analitiche. Delle volte, fa comodo avere i risultati numerici e quindi ho utilizzato nella linea %i67 il modificatore numer, che indica al programma di presentare i risultati in forma numerica, che poi ho fatto scrivere in forma estesa utilizzando expand; Fino a qui, niente di particolare. Diventa più interessante calcolare tutte le radici di un polinomio di grado alto. Non è un problema che nel caso generale è risolvibile analiticamente, quindi anche Maxima propone la funzione allroots(), che permette di fare i calcoli numericamente (ottenendo al massimo circa 16 cifre significative, se il problema non è mal condizionato, cosa che purtroppo accade spesso).
Ecco un esempio di grado 12 (che ho preso da un mio libro di elettronica, per verificare il risultato):
%i71) p: 1+2*x^3+2*x^6+2*x^9+x^12;
12 9 6 3
(%o71) x + 2 x + 2 x + 2 x + 1
(%i72) allroots(p=0);
(%o72) [x = .8660254151728854 %i + .5000000152932945,
x = .5000000152932945 - .8660254151728854 %i,
x = .4999999999999991 %i - .8660254037844395,
x = - .4999999999999991 %i - .8660254037844395,
x = .9999999999999994 %i + 5.866392267360735E-16,
x = 5.866392267360735E-16 - .9999999999999994 %i,
x = .8660253923959913 %i + .4999999847067038,
x = .4999999847067038 - .8660253923959913 %i,
x = .5000000000000003 %i + .8660254037844387,
x = .8660254037844387 - .5000000000000003 %i, x = - .9999999683898616,
x = - 1.000000031610135]
(%i73)
Confrontando i risultati, si vede che la precisione che si ottiene è di circa 7-8 cifre (è banale osservare che x=-1 è soluzione). Problemi come questi non sono banali ed è sempre buona norma darsi gli strumenti per controllare la loro efficacia, per esempio provando altri metodi numerici e confrontando i risultati.
Un esempio pratico: la prova di Hurwitz
I polinomi sono spesso utilizzati in molti campi e le loro proprietà dipendono in molti contesti dalla posizione delle radici sul piano complesso. Purtroppo, come abbiamo visto, fare calcoli con polinomi di grado alto è difficile e procedendo solo per via numerica può capitare che le approssimazioni si facciano sentire in modo preoccupante. Spesso però, quello che serve è solamente osservare la parte reale delle radici, per vedere se è positiva, nulla o negativa, per delle ragioni legate alla stabilità di un sistema. Per un polinomio con soluzioni reali, basta la nota regoletta dei segni di Cartesio. Quando però si prendono in considerazione soluzioni in campo complesso questa regola non funziona più e bisogna ricorrere ad una prova matematica più complessa denominata prova di Hurwitz.
La prova di Hurwitz è un algoritmo puramente algebrico che consente di osservare se un polinomio ha tutte le radici con parte reale non positiva (polinomio hurwitziano in senso lato), oppure negativa (polinomio strettamente hurwitziano). Vediamo qui come effettuare la prova di Hurwitz utilizzando Maxima. Ecco il polinomio di partenza, preso sempre dal mio libro di teoria delle reti elettriche (uso p per indicare la pulsazione complessa, occhio che non deve essere stata definita prima):
(%i95) kill(p);
(%o95) done
(%i96) M(p):=56*p^5+7*p^4+161*p^3+18*p^2+98*p+8;
5 4 3 2
(%o96) M(p) := 56 p + 7 p + 161 p + 18 p + 98 p + 8
(%i97)
Si noti che ho definito M(p) come una funzione dipendente dalla variabile p, grazie all'operatore :=
La parte pari di un polinomio è il polinomio formato da tutti i termini con potenza di p pari mentre la parte dispari è ovviamente quella che ha tutti i termini con potenza di p dispari. Bisogna procedere per divisioni successive dividendo la parte pari per la parte dispari del polinomio o viceversa, a seconda di quella che ha il grado più elevato. Ovviamente, si ottiene un termine di solito di grado 1, più un resto. Con Maxima è semplice estrarre parte pari e dispari di un polinomio, basta ricordare alcune proprietà ed in particolare le seguenti:
(%i105) M(p):=56*p^5+7*p^4+161*p^3+18*p^2+98*p+8;
5 4 3 2
(%o105) M(p) := 56 p + 7 p + 161 p + 18 p + 98 p + 8
(%i106) Pa(p):=1/2*(M(p)+M(-p));
1
(%o106) Pa(p) := - (M(p) + M(- p))
2
(%i107) Di(p):=1/2*(M(p)-M(-p));
1
(%o107) Di(p) := - (M(p) - M(- p))
2
(%i108) expand(Pa(p));
4 2
(%o108) 7 p + 18 p + 8
(%i109) expand(Di(p));
5 3
(%o109) 56 p + 161 p + 98 p
(%i110)
Bene. Incominciamo con le derivate successive. Dividiamo Di(p) per Pa(p), perché la prima ha grado più alto. La funzione da utilizzare è divide, che vuole il numeratore, il denominatore e la variabile principale del polinomio (dato che possono essercene diverse):
(%i110) divide(Di(p),Pa(p),p);
3
(%o110) [8 p, 17 p + 34 p]
(%i111)
Il risultato è scritto sotto forma di lista, ovvero una serie di elementi racchiusi fra parentesi quadre. Il primo elemento è il risultato, il secondo è il resto. La prova di Hurwitz consiste a continuare le divisioni successive, questa volta fra la parte pari ed il resto (che è dispari). Si accede al resto prendendo il secondo elemento della lista e facendo la divisione:
(%i128) Di1(p):=second(%o110);
(%o128) Di1(p) := second(%o110)
(%i129) Di1(p);
3
(%o129) 17 p + 34 p
(%i130) divide(Pa(p), Di1(p),p);
7 p 2
(%o130) [---, 4 p + 8]
17
(%i131)
Si continua così fino a che non rimane più nulla da dividere:
(%i131) Pa1(p):=second(%o130);
(%o131) Pa1(p) := second(%o130)
(%i132) Pa1(p);
2
(%o132) 4 p + 8
(%i133) divide(Di1(p),Pa1(p),p);
17 p
(%o133) [----, 0]
4
(%i134)
Si sono ottenuti quindi come quozienti di primo grado 8p, 7/17p e 17/4p. Sono tutti positivi, ma sono solo tre invece di cinque (il grado del polinomio di partenza). Il polinomio dato è hurwitziano in senso lato.
Il testo da cui ho preso gli esempi è "Sintesi dei circuiti passivi", di Claudio Beccari edito da CLUT.
Calcoli con precisione arbitraria
Tanto per restare in tema, l'operatore bfloat() permette di definire tutti gli elementi dell'espressione che è stata fornita come dei big float, ovvero dei numeri in virgola mobile anche molto lunghi. Il numero di cifre è stabilito dal valore della variabile fpprec. Ecco come stampare le prime cinquantamila cifre di pi greco (ci vuole un po' di tempo):
(%i143) fpprec:50000; (%o143) 50000 (%i144) bfloat(%pi); (%o144) 3.1415926535897... Qui taglio, sennò riempio troppo spazio ...712307568610450045489703600795698276263923441071465848957802414081584052295\ 369374997106655948944592462866199635563506526234053394391421112718106910522900\ 24657423488b0
Per la cronaca, ho controllato con questo sito, che riporta i primi 4 milioni di decimali ed il risultato è corretto nell'ambito della precisione richiesta: http://zenwerx.com/pi.php
Calcolo matriciale e composizione con TeX
In questa sezione, vedremo brevemente come fare qualche calcolo con le matrici e come utilizzare TeX per mostrare i risultati.
Ecco uno dei modi per definire una matrice: il comando entermatrix, che vuole come argomento le dimensioni:
(%i154) a: entermatrix(4,4);
Is the matrix 1. Diagonal 2. Symmetric 3. Antisymmetric 4. General
Answer 1, 2, 3 or 4 :
4;
Row 1 Column 1:
k^2-1;
Row 1 Column 2:
3
;
Row 1 Column 3:
1;
Row 1 Column 4:
1;
Row 2 Column 1:
5;
Row 2 Column 2:
3;
Row 2 Column 3:
2;
Row 2 Column 4:
1;
Row 3 Column 1:
k;
Row 3 Column 2:
2;
Row 3 Column 3:
1;
Row 3 Column 4:
-1;
Row 4 Column 1:
k;
Row 4 Column 2:
-1;
Row 4 Column 3:
2;
Row 4 Column 4:
0;
Matrix entered.
[ 2 ]
[ k - 1 3 1 1 ]
[ ]
(%o154) [ 5 3 2 1 ]
[ ]
[ k 2 1 - 1 ]
[ ]
[ k - 1 2 0 ]
(%i155)
Dapprima viene chiesto il tipo di matrice e poi si procede elemento per elemento. Da notare che non si è limitati ad input numerici, ma si possono anche utilizzare delle variabili, come per esempio k. Rappresentiamo con il TeX il risultato:
(%i156) tex(a);
$$\pmatrix{k^2-1&3&1&1\cr 5&3&2&1\cr k&2&1&-1\cr k&-1&2&0\cr }$$
Il codice racchiuso fra il doppio dollaro $$ è l'espressione scritta nel formato TeX. Per chi non conoscesse TeX e LaTeX, si veda qui:
http://it.wikipedia.org/wiki/TeXhttp://it.wikipedia.org/wiki/LaTeX
Io ho una versione di teTeX installata a cui ho aggiunto alcuni pacchetti. Per comodità, alle volte utilizzo un softwarino per Macintosh molto carino, LaTeXiT:
http://ktd.club.fr/programmation/latexit_en.php
Questo programma (che va affiancato ad una distribuzione LaTeX funzionante) permette di scrivere un'equazione e fare molto comodamente copia/incolla in presentazioni, testi o salvare l'immagine.
Il solo problema che ho incontrato è che il codice generato da Maxima segue le vecchie convenzioni TeX puro ed ho per esempio dovuto disattivare il pacchetto amsmath modificando il preambolo standard usato da LaTeXiT, escludendo questo pacchetto.
Ad ogni modo, ecco il risultato:
Già: TeX e LaTeX sono considerati attualmente fra i migliori sistemi al mondo per la composizione automatica delle equazioni. In ogni istante si può ottenere il codice TeX ed ottenere l'immagine dell'espressione senza fare nessuno sforzo.
Proseguiamo. Ecco il calcolo della matrice inversa con il comando invert; può risultare comodo tenere a fattore comune il determinante con l'opzione detout:
(%i160) invert(a);
[ 13 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ k - 10 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
(%o160) Col 1 = [ ]
[ - 6 k - 5 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 9 k - 25 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ 12 ]
[ - ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ 2 (k - 1) ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
Col 2 = [ ]
[ 2 ]
[ k + 6 k - 1 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ 5 (k - 1) - 6 k ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ 1 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ 2 (k - 1) + k - 10 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
Col 3 = [ ]
[ 2 ]
[ k - 6 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ - 8 (k - 1) + 3 k + 3 (10 - 2 k) + 5 ]
[ ------------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ 5 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ - 3 (k - 1) - k + 10 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
Col 4 = [ ]
[ 2 ]
[ 5 (k - 1) + 3 k + 3 (- k - 5) - 10 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
[ ]
[ 2 ]
[ - k - 3 k - 3 (5 - 2 k) + 11 ]
[ ----------------------------------- ]
[ 2 ]
[ 13 (k - 1) + 3 k + 3 (k - 10) - 30 ]
(%i161)
Si noti come il risultato venga fornito colonna per colonna. Facciamo la prova che la matrice per la sua inversa dia la matrice identità:
(%i168) a . b;
[ 2 ]
[ k - 1 3 1 1 ]
[ ]
(%o168) [ 5 3 2 1 ] . (matrix([13, - 12, 1, 5],
[ ]
[ k 2 1 - 1 ]
[ ]
[ k - 1 2 0 ]
2 2 2
[k - 10, 2 (k - 1), 2 (k - 1) + k - 10, - 3 (k - 1) - k + 10],
2 2 2
[- 6 k - 5, k + 6 k - 1, k - 6, 5 (k - 1) + 3 k + 3 (- k - 5) - 10],
2 2
[9 k - 25, 5 (k - 1) - 6 k, - 8 (k - 1) + 3 k + 3 (10 - 2 k) + 5,
2 2
- k - 3 k - 3 (5 - 2 k) + 11])/(13 (k - 1) + 3 k + 3 (k - 10) - 30))
(%i169) c:expand(a . b);
[ 2 ]
[ 13 k 6 k 73 ]
[ ---------------- + ---------------- - ---------------- ]
[ 2 2 2 ]
[ 13 k + 6 k - 73 13 k + 6 k - 73 13 k + 6 k - 73 ]
(%o169) Col 1 = [ ]
[ 0 ]
[ ]
[ 0 ]
[ ]
[ 0 ]
[ 0 ]
[ ]
[ 2 ]
[ 13 k 6 k 73 ]
[ ---------------- + ---------------- - ---------------- ]
Col 2 = [ 2 2 2 ]
[ 13 k + 6 k - 73 13 k + 6 k - 73 13 k + 6 k - 73 ]
[ ]
[ 0 ]
[ ]
[ 0 ]
[ 0 ]
[ ]
[ 0 ]
[ ]
[ 2 ]
Col 3 = [ 13 k 6 k 73 ]
[ ---------------- + ---------------- - ---------------- ]
[ 2 2 2 ]
[ 13 k + 6 k - 73 13 k + 6 k - 73 13 k + 6 k - 73 ]
[ ]
[ 0 ]
[ 0 ]
[ ]
[ 0 ]
[ ]
[ 0 ]
Col 4 = [ ]
[ 2 ]
[ 13 k 6 k 73 ]
[ ---------------- + ---------------- - ---------------- ]
[ 2 2 2 ]
[ 13 k + 6 k - 73 13 k + 6 k - 73 13 k + 6 k - 73 ]
(%i170)
L'operatore prodotto fra matrici è il punto. Non si ottiene la matrice identità (o almeno così non sembra) perché i termini non sono fattorizzati, problema a cui si rimedia con il comando factor:
(%i174) factor(c);
[ 1 0 0 0 ]
[ ]
[ 0 1 0 0 ]
(%o174) [ ]
[ 0 0 1 0 ]
[ ]
[ 0 0 0 1 ]
(%i175)
Naturalmente, si può benissimo calcolare autovalori (eigenvalues in inglese) o autovettori (eigenvectors) con i comandi eigenvectors(a) ed eigenvalues(a), ma non riporto l'output perché è molto lungo.
Per finire, ecco un esempio di un'altra espressione ottenuta grazie a TeX, un integrale questa volta:
(%i187) i:'integrate((x^2+2*x+1)/(x-2),x);
/ 2
[ x + 2 x + 1
(%o187) I ------------ dx
] x - 2
/
(%i188) o:integrate((x^2+2*x+1)/(x-2),x);
2
x + 8 x
(%o188) 9 log(x - 2) + --------
2
(%i189) tex(i=o);
$$\int {{{x^2+2\,x+1}\over{x-2}}}{\;dx}=9\,\log \left(x-2\right)+{{x^2
+8\,x}\over{2}}$$
(%o189) false
(%i190)
Qui ho usato il comando integrate due volte: la prima per calcolare la primitiva e la seconda per farmi scrivere l'espressione. Si noti che ho usato l'operatore ' (apice) che impedisce a Maxima di svolgere l'integrazione, ma la lascia non elaborata, di modo da ottenere il codice TeX corrispondente. Ecco il risultato:
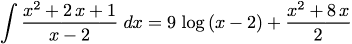
(ah... l'uguaglianza è vera, ma nel caso generale ci vuole una costante arbitraria nella primitiva).
P.S. Nell'ultima immagine ottenuta con TeX, vedo un piccolo bug. Secondo le norme internazionali, la 'd' del differenziale non deve essere in corsivo, ma in tondo. Comunque, si tratta di un errore che ho trovato anche in diverse pubblicazioni. Basta sostituire a mano la 'd' nell'espressione TeX con {\rm d} per risolvere il problema.
Qualche esempio di analisi
Abbiamo già visto che Maxima non si fa problemi a calcolare primitive e derivate:
(%i194) f:sin(x)/(atan(x)+x^2);
sin(x)
(%o194) ------------
2
atan(x) + x
(%i195) g:diff(f,x);
1
(------ + 2 x) sin(x)
2
cos(x) x + 1
(%o195) ------------ - ---------------------
2 2 2
atan(x) + x (atan(x) + x )
(%i196) 'integrate(g,x)=integrate(g,x);
1
(------ + 2 x) sin(x)
/ 2
[ cos(x) x + 1
(%o196) I (------------ - ---------------------) dx =
] 2 2 2
/ atan(x) + x (atan(x) + x )
cos(x) sin(2 x) - sin(x) cos(2 x) + sin(x)
-------------------------------------------------------
2 2 2 2
(2 atan(x) + 2 x ) sin (x) + (2 atan(x) + 2 x ) cos (x)
(%i197) 'integrate(g,x)=trigreduce(integrate(g,x));
1
(------ + 2 x) sin(x)
/ 2
[ cos(x) x + 1 sin(x)
(%o197) I (------------ - ---------------------) dx = ------------
] 2 2 2 2
/ atan(x) + x (atan(x) + x ) atan(x) + x
(%i198) tex(%);
$$\int {{{\cos x}\over{\arctan x+x^2}}-{{\left({{1}\over{x^2+1}}+2\,x
\right)\,\sin x}\over{\left(\arctan x+x^2\right)^2}}}{\;dx}={{\sin x
}\over{\arctan x+x^2}}$$
(%o198) false
(%i199)
Ho estratto il codice TeX alla linea %o198, che produce come risultato:
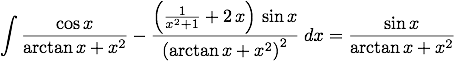
(con la solita costante arbitraria che manca per il caso generale...). Naturalmente, si può facilmente calcolare anche dei limiti con il comando limit; vediamone uno facile: il limite per x che tende a zero di k*sin(x)/x.
(%i202) f:k*sin(x)/x;
k sin(x)
(%o202) --------
x
(%i203) limit(f,x,0);
(%o203) k
(%i204)
Vediamo ancora qualche esempio, per esempio con la funzione tangente:
(%i3) limit(tan(x),x,%pi/2); (%o3) und (%i4) limit(tan(x),x,%pi/2,plus); (%o4) minf (%i5) limit(tan(x),x,%pi/2,minus); (%o5) inf
Nel primo caso, si è calcolato il limite della tangente per x che tende verso pi/2. Maxima risponde correttamente che tale limite non esiste (und corrisponde a undefined). Si sono quindi calcolati i limiti destro e sinistro allo stesso punto singolare, ottenendo meno infinito (minf), oppure più infinito (inf).
Il limite è svolto utilizzando alcune sostituzioni che alla fine portano ad una libreria di limiti notevoli, oppure confrontando gli ordini di infinito/infinitesimo. Il manuale di Maxima fornisce come riferimento una tesi di dottorato molto interessante:
http://www.lcs.mit.edu/publications/specpub.php?id=660
La cosa divertente è che il relatore è stato Seymour Papert, il papà del LOGO.
Esiste alternativamente le funzione tlimit(), che calcola il limite utilizzando uno sviluppo in serie di Taylor o di Laurent.
Attenzione però che in alcuni casi se la funzione ha un comportamento patologico, si può mettere in crisi Maxima. Ecco un esempio:
(%i58) p:(log(1+%e^(1/x))*sin(x^7))/((1/(1-x^2))^(sin(x)^2)-1-x^4);
7 1/x
sin(x ) log(%e + 1)
(%o58) ------------------------
1 4
--------------- - x - 1
2
2 sin (x)
(1 - x )
(%i59) limit(factor(p(x)),x,0,minus);
^CMaxima encountered a Lisp error:
EXT:GC: User break
Automatically continuing.
To reenable the Lisp debugger set *debugger-hook* to nil.
(%i60) limit(factor(p(x)),x,0,plus);
2 2
sin (x) log(1 - x ) 7 1/x
%e sin(x ) log(%e + 1)
(%o60) - limit --------------------------------------------
x -> 0+ 2 2
4 2 sin (x) 2 sin (x)
x (1 - x ) + (1 - x ) - 1
(%i61) tlimit(factor(p(x)),x,0,plus);
(%o61) 0
(%i62) tlimit(factor(p(x)),x,0,minus);
(%o62) 0
(%i63)
Quando ho lanciato il comando limit(factor(p(x)),x,0,minus);, Maxima si è messo a lavorare intensivamente per un po', fino a che mi sono stufato e l'ho interrotto con un CTRL-C.
Il comando tlimit sembra incontrare meno problemi e fornisce zero quasi subito, ma il risultato E' SBAGLIATO!!!
Il limite per x che tende a zero più della funzione che ho fornito è infatti 6. Lo si dimostra sviluppando in serie di Taylor un po' più in profondità rispetto a quanto non si faccia di solito. Ad ogni modo, la funzione ha un comportamento un parecchio ostico attorno all'origine, come si vede dal suo grafico:
(%i80) plot2d(p(x), [x, -0.1,.1], [gnuplot_term, aqua]);
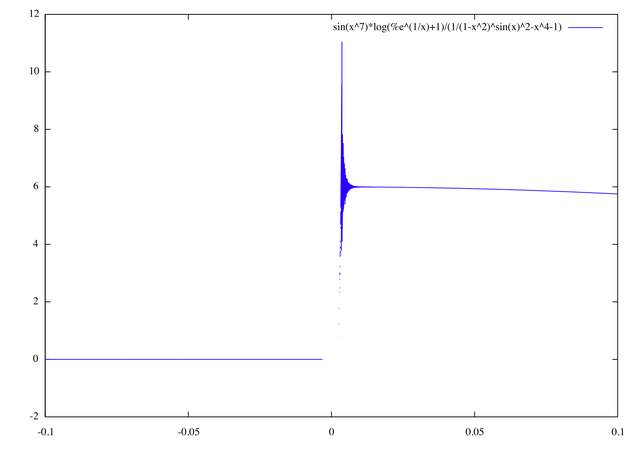
Una cosa comoda in questi casi, ma sempre da usare con attenzione, è il comando taylor, che consente appunto di sviluppare secondo Taylor o secondo Laurent in un intorno di un punto singolare fino ad un ordine prefissato.
Il manuale ci dice:
taylor (expr, x, a, n) expands the expression expr in a truncated Taylor or Laurent series in the variable x around the point a, containing terms through (x - a)^n.Ecco un esempio applicato al nostro caso:
(%i81) p:(log(1+%e^(1/x))*sin(x^7))/((1/(1-x^2))^(sin(x)^2)-1-x^4);
7 1/x
sin(x ) log(%e + 1)
(%o81) ------------------------
1 4
--------------- - x - 1
2
2 sin (x)
(1 - x )
(%i82) taylor(p(x),x,0,1);
(%o82)/T/ 0 + . . .
(%i83) taylor(p(x),x,0,2);
(%o83)/T/ 0 + . . .
(%i84) taylor(p(x),x,0,3);
(%o84)/T/ 0 + . . .
(%i85) taylor(p(x),x,0,4);
(%o85)/T/ 0 + . . .
(%i86) taylor(p(x),x,0,5);
(%o86)/T/ 0 + . . .
(%i87) taylor(p(x),x,0,6);
6
(%o87)/T/ x + . . .
(%i88) taylor(p(x),x,0,7);
2 4 6
128 x 51209 x 2021759 x
(%o88)/T/ 6 - ------ + -------- - ---------- + . . .
5 525 5250
3 5 7
128 x 51209 x 2021759 x - 1/x
+ (6 x - ------ + -------- - ---------- + . . .) %e
5 525 5250
3 5 7
64 x 51209 x 2021759 x - 1/x 2
+ (- 3 x + ----- - -------- + ---------- + . . .) (%e )
5 1050 10500
3 5 7
128 x 51209 x 2021759 x - 1/x 3
+ (2 x - ------ + -------- - ---------- + . . .) (%e )
15 1575 15750
3 5 7
3 x 32 x 51209 x 2021759 x - 1/x 4
+ (- --- + ----- - -------- + ---------- + . . .) (%e )
2 5 2100 21000
3 5 7
6 x 128 x 51209 x 2021759 x - 1/x 5
+ (--- - ------ + -------- - ---------- + . . .) (%e )
5 25 2625 26250
3 5 7
64 x 51209 x 2021759 x - 1/x 6
+ (- x + ----- - -------- + ---------- + . . .) (%e )
15 3150 31500
3 5 7
6 x 128 x 51209 x 2021759 x - 1/x 7
+ (--- - ------ + -------- - ---------- + . . .) (%e ) + . . .
7 35 3675 36750
(%i89)
Si ottiene un risultato utilizzabile soltanto quando abbiamo forzato il calcolo del polinomio di Taylor almeno fino al settimo grado. Il motivo per cui vengono riportati anche dei termini esponenziali che non sono sviluppati credo sia dovuto al fatto che e^(1/x) è decisamente un oggetto da trattare con molto rispetto nell'intorno di zero e quindi il programma non tenta di svilupparlo. Si noti che quest'espressione è uguale a 6 per x reale che tende verso zero positivo.
Ho fatto questi commenti per fare vedere come anche usando strumenti automatici, bisogna sempre fare molta attenzione ed avere ben presente la sostanza del problema prima ancora di introdurlo. Parafrasando qualcuno che conosco: per usare un programma di calcolo simbolico, bisogna saper fare i calcoli meglio di lui.
Definire una funzione in Maxima
Maxima può essere esteso definendo delle funzioni aggiuntive che possono essere usate in maniera analoghe a quelle definite dal programma. Vi sono due possibilità
- scrivere funzioni adottando la sintassi di Maxima
- scrivere funzioni in Lisp
Noi forniremo un piccolo esempio di funzione abbastanza completa scritta utilizzando i comandi di Maxima. L'obiettivo è quello di automatizzare la prova di Hurwitz descritta precedentemente. Ecco il codice:
/* Perform the Hurwitz test on the M(p) polynomials using Maxima
Version 1.0
Written by Davide Bucci, March-April 2007
This program is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program; if not, write to the Free Software
Foundation, Inc., 51 Franklin St, Fifth Floor, Boston, MA 02110-1301 USA
*/
/* Qualche esempio di polinomio hurwitziano e non:
-----------------------------------------------
56*p^5+7*p^4+161*p^3+18*p^2+98*p+8, Hurwitziano in senso lato
p^3+2*p^2+4*p+3, Strettamente hurwitziano
p^5+2*p^4+2*p^3+4*p^2+11*p+10, Non hurwitziano
p^3+2*p^2+4*p+9, Non hurwitziano
*/
hurwitz(poly,var):=block ([M,p],
/* Definiamo una funzione che ci permettera' di lavorare sul nostro
polinomio in maniera generale, utilizzando la variabile var */
define(M(var),poly),
if(debugmode) then print(M(p)),
print("Prova di Hurwitz per un polinomio"),
/* Otteniamo parte pari e dispari del polinomio */
Pa(p):=expand(1/2*(M(p)+M(-p))),
Di(p):=expand(1/2*(M(p)-M(-p))),
/* Abbiamo bisogno di ottenere il grado piu' elevato al numeratore */
pg:hipow(Pa(p), p),
dg:hipow(Di(p), p),
num:Di(p),
den:Pa(p),
nm:dg,
if (pg>dg) then
(num:Pa(p), den:Di(p), nm:pg),
if (den#0) then (
res:divide(num,den,p),
/* Adesso possiamo effettuare le divisioni successive */
hasdivided: (second(res)#0),
print(hasdivided),
/* This list will contain the results of the successive divisions */
reslist:[],
ishurwitz:true,
print("Calcolo delle divisioni successive"),
for i:0 thru nm while (hasdivided and ishurwitz) do (
if(debugmode) then (
print("nuova iterazione"),
print(i),
print("divide"),
print(num),
print("by"),
print(den)
),
res:divide(num,den,p),
if(debugmode) then (
print("resulting"),
print(res)
),
hasdivided: (second(res)#0),
reslist:append(reslist,[first(res)]),
num:expand(den),
den:second(res),
/* Si controlla se il risultato della divisione e' un monomio di grado 1
con coefficiente positivo */
if (hipow(first(res),p)>1) then (
ishurwitz:false
),
if (coeff(first(res),p,1)<0) then (
ishurwitz:false
)
),
if (length(reslist)=nm and ishurwitz) then
print("Polinomio strettamente hurwitziano")
elseif (ishurwitz) then
print("Polinomio hurwitziano in senso lato")
else
print("Polinomio non hurwiztiano"),
print(reslist),
reslist
) else
print("Polinomio solo pari o solo dispari")
)$
Rispetto all'uso normale di Maxima attraverso la linea di comando, si vedono alcune differenze. Quella che salta più all'occhio è che per separare le diverse istruzioni si usa la virgola e non il punto e virgola.
Questa funzione va scritta in un file che chiameremo Hurwitz.max e che supporrò per semplicità presente nella directory corrente. Per fare in modo che Maxima carichi la funzione, bisogna utilizzare il comando load, indicando il nome del file. Dopodichè, si potrà accedere alla funzione hurwitz(pol, var), come nell'esempio seguente:
(%i5) load("Hurwitz.max");
(%o5) Hurwitz.max
(%i6) hurwitz(56*p^5+7*p^4+161*p^3+18*p^2+98*p+8,p);
Prova di Hurwitz per un polinomio
3
17 p + 34 p # 0
Calcolo delle divisioni successive
Polinomio hurwitziano in senso lato
7 p 17 p
[8 p, ---, ----]
17 4
7 p 17 p
(%o6) [8 p, ---, ----]
17 4
(%i7)
Conclusioni
Con questo intervento, più che fornire una descrizione sistematica delle notevoli possibilità offerte da Maxima, ho cercato di fornire una collezione di esempi commentati che possono fornire qualche ispirazione. Si tratta tuttavia di un programma molto complesso e gli esempi trattati non fanno che scalfire appena la superficie di un vasto mondo... Buona ricerca!License:
--------
Copyright (C) 2007-2008 Davide Bucci davbucci at tiscali dot it
This program is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program; if not, write to the Free Software
Foundation, Inc., 675 Mass Ave, Cambridge, MA 02139, USA.
