Le problème de la gamme musicale
Difficultés dans la création d'un système organiqueL'introduction du système tempéré
Une mesure de hauteur : la gamme des cents
Conclusion
Bibliographie
Difficultés dans la création d'un système organique
La très grande majorité de la musique actuelle est basée sur le concepte de gamme chromatique, c'est à dire sur l'ensemble de regle qui par exemple existent derriere le choix des fréquences de chaque corde de guitare ou de piano. La question n'est pas simple du tout : les différents gammes sont basées essentiellement sur des conventions et on a eu un grand nombre d'efforts dans l'histoire de la musique pour codifier dans un système suffisamment flexible et précis les différents intervalles qui constituent la structure sur laquelle le compositeur fonde son ouvrage.
Sans vouloir parcourir en détail toute l'histoire de la musique, il est suffisant de rappeler comme la gamme (c'est à dire l'ensemble des intervalles qui sont à la base de la composition) a connu une première codification avec les grecs et leurs "modes" qui ont été utilisés fondamentalement jusqu'au XVI siècle avec les études de V. Galilei, N. Tartini et, surtout, G. Zarlino. Ce dernier en particulier fit la proposition d'une gamme basée sur des rapports simples de fréquence dans laquelle, par exemple, un intervalle d'une cinquième (entre do et sol) est caractérisé par un rapport de 3/2 entre les fréquences des notes qui le constituent.
Avec un ensemble de constructions similaires (cinquièmes ascendantes et quatrièmes descendantes), on peut arriver à définir tous les degrés de la gamme diatonique (do, re, mi, fa, sol, la, si). Le plus grand problème qui se présentait avec ce système était la difficulté d'accordage des démitons dans les instruments à intonation fixe comme le clavecin : en particulier, deux notes enharmoniques comme le do dièse et le re bémol (qui correspondent à la même touche noire du clavier) ont deux fréquences différentes.
L'introduction du système tempéré
Pour résoudre ce problème, qui était vite devenu très lourd suite au développement du goût harmonique et aux nécessités musicales, a été proposée par A. Werckmeister la construction d'une gamme qui "tempérait" les différences entre les démitons de façon à avoir le même son associé soit au démiton chromatique qu'au démiton diatonique et donc, finalement à "tempérer" la différence entre deux notes comme le do dièse et le re bémol, utilisé pour la première fois par J. S. Bach qui dans le 1722 et 1744 écrit les deux livres du "Clavecin bien tempéré" qui sont encore aujourd'hui considérés comme des ouvrages fondamentales dans la pédagogie musicale. La construction est très simple : on considère l'intervalle d'octave (celui qui se trouve entre deux do successifs sur un clavier) comme le rapport 2 des fréquences on peut donc déterminer les fréquences des degrés intermédiaire en adoptant une progression géométrique qui divise en 12 l'intervalle d'octave, selon ce principe on arrive à définir que la fréquence d'une note est égale à celle du démi-ton précédent multipliée par la racine douzième de deux.
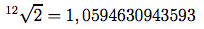
Parallèlement à la codification de la gamme, on vit croître la nécessité d'adopter un son d'intonation fixe et suffisamment reproductible comme référence pour constituer les intervalles de la gamme. Ce choix est largement arbitraire et depuis le XVIII siècle la fréquence de référence a connu un lent mais progressif décalage vers le haut pour être fixée seulement dans le XX siècle avec un ensemble de normes (après des discussions qui ont durées plusieurs dizaines d'années. . .) et des conventions internationales. Le choix a été de fixer la note La3 à 440 Hz avec une tolérance de plus ou moins 0, 5 Hz.
Avec l'adoption du système tempéré et du La3 à 440 Hz, on peut calculer très facilement le tableau suivant, qui montre les fréquences associées à la gamme tempérée, sur un intervalles de cinq octaves. En noir, il y a les notes associées aux six cordes d'une guitare.
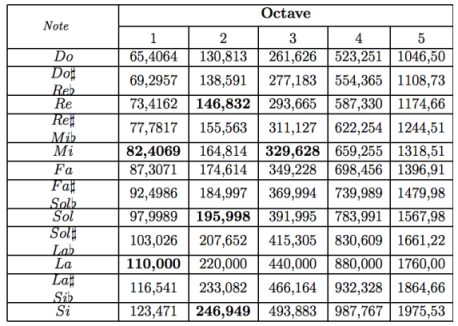
Il faut néanmoins mettre en évidence les limites d'un tel système qui se fonde sur une construction de type mathématique, c'est à dire :
- l'oreille n'est pas du tout linéaire même dans la perception de la hauteur de la note, où elle joue un rôle de très grande importance aussi la durée temporelle du phénomène acoustique
- la musique est un art : dans un piano à code qui vient d'être accordé à règle d'art par une oreille d'un accordeur professionnel il y aura toujours des très petites différences avec les calculs théoriques ; ces différences, loin d'être des erreurs sont importantes pour obtenir un "bon" son
- dans certaines courants de la musique contemporaine, le rôle de la gamme devient moins importante, suite aux recherches sur les micro-intervalles et le bruit (L. Nono, J. Cage, L. Berio)
- dans l'exécution des partition anciennes avec des critères de philologie, on utilise pour des chorales ou des instruments à arcs un diapason différent (430Hz ou 415Hz, diapason baroque) et, plus rarement, la gamme naturelle
Une mesure de hauteur : la gamme des cents
Quand on parle des intervalles qui ne peuvent pas être quantifiés exacte- ment sur la gamme tempérée, il est utile d'introduire une subdivision beaucoup plus fine qui nous permet d'identifier des rapports de hauteur avec une très grande précision. L'idée qui a été suivie est celle d'appliquer le même principe qui règle la construction de la gamme tempérée, avec un nombre très grand de pas, de façon à diviser finement les intervalles. Une mesure de ce type est la gamme des cents qui subdivise l'octave (rapport 2 entre les fréquences) en 1200 de façon à diviser par 100 le démiton tempéré. Cette proposition a été faite à la fin du XIX siècle par Ellis et il s'agit, comme la gamme tempérée, d'une progression géométrique cette fois en base racine 1200-ème de 2 :
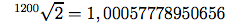
ce rapport est donc celui qui se trouve entre deux fréquences distancées d'un cent. La sensibilité aux variations de hauteur d'une oreille humaine varie beaucoup sur une base statistique et peut arriver jusqu'à 2 cents dans des situations idéales, sons purs et un individu musicalement éduqué. Dans des conditions normales, une imprécision de 8 cents est plus que suffisant et on peut mesurer que les oscillations en hauteur d'une orchestre parfaitement accordée peuvent arriver jusqu'à une dizaine de cents, sans que cela puisse constituer aucun problème.
Conclusion
Avec cet article, nous avons cherché de donner une première idée de la formation mathématique de la gamme tempérée et des systèmes utilisés pour mesurer les intervalles dans la théorie musicale moderne. Bien évidemment, il s'agit d'un domaine très complexe. Dans la suite, nous indiquons quelques bouquins particulièrement intéressant à ce propos.
Bibliographie
P. Righini - L'acustica per il musicista, Fondamenti fisici della musica, VIII edizione, Zanibon, 1994A. Baines - Storia degli strumenti musicali, prima edizione italiana Biblioteca Universale Rizzoli, 1995
