Maths

Even if I am not a professionally trained mathematician, maths is fundamental for my work and I always enjoyed it a lot. For this reason, I decided to group here a few articles related to it.


	How to draw Mandelbrot and Julia fractals (1998-2002), IT In this article, written long ago, I described a practical way to draw on a computer the Mandelbrot and Julia fractal sets.
	Mandelbrot and Julia sets in Java (2004), FR, IT A practical example based on the first article: two Java applets to draw Mandelbrot and Julia sets, directly inside the browser. They are open source, so you can download their source code.
	Analsysis 2.3beta2 (1998-2002), FR, IT I wrote Analysis many years ago for the Microsoft Windows operating system. I worked on this software, dedicated to function plotting, from 1997 to 2002. Some might still find it interesting since it is quite small and easy to use.
	Introduction to Maxima (2007), FR, IT Maxima is an open source version (GPL'ed) of the Macsyma project. Macsyma was the first algebraic manipulation language developed at the MIT between 1960's to mid 1980's. I tried to put together several real life examples, in order to have a rough idea of the flexibility and the power of this software.
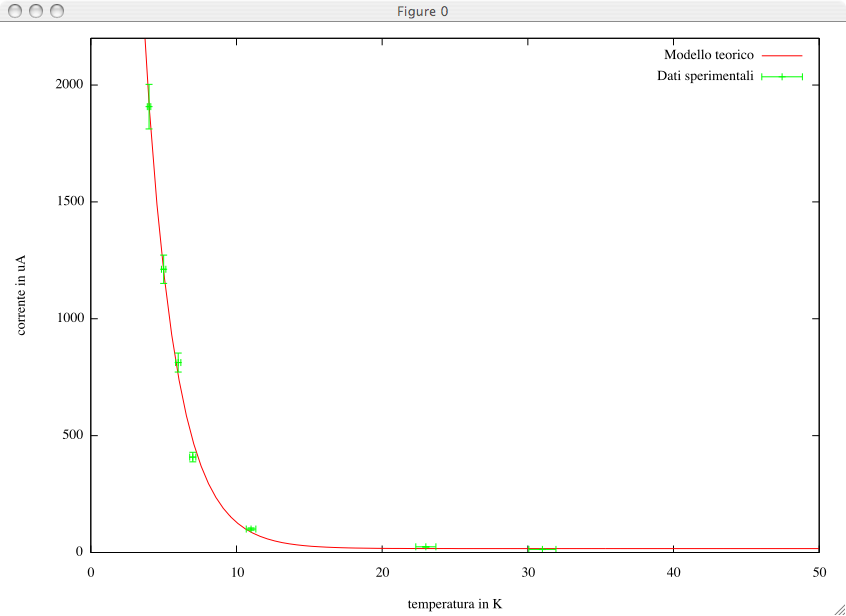
	Introduction to Gnuplot (2007-2008), FR, IT Gnuplot is a widely used software for graphical plotting of scientific data. If it is correctly used, it can give very professional results, of typographic quality. In this article, we comment several more or less complex examples.
	The mathematical symmetry of the differential pair (2011) I wrote this article for my blog on the italian site ElectroYou. The study is devoted to the transistor differential pair. In particular, it is shown that the effect of the circuit in linearity on the input signals can be interpreted as the result of a linear application. This application can be described via an appropriate matrix. It is demonstrated that the diagonalization of this matrix (by calculating eigenvalues and eigenvectors) yields naturally to the well known concepts of differential and common modes. This article has been written in english, a few days before Christmas 2011.